Cho một hỗn hợp kim loại AB nặng 24kg có chiều dài là 3,6m được dùng là dàn giáo xây dựng bắc ngang qua hai điểm tỳ. Trọng tâm của hỗn hợp kim loại cách điểm tựa A là 2,4m, cách B là 1,2m. Xác định lực mà tấm hỗn hợp kim loại tác dụng lên 2 điểm tỳ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
15 tháng 11 2019
Ta có trọng lực của thanh P = m g = 24.10 = 240 ( N )
Gọi Lực tác dụng ở điểm A là P1 cách trọng tâm d1
Lực tác dụng ở điểm A là P2 cách trọng tâm d2
Vì F → 1 ; F → 2 cùng phương cùng chiều nên P= F1 + F2 = 240N F1 = 240 – F2
Áp dụng công thức: F1.d1 = F2.d2 ( 240 – F2).2,4 = 1,2.F2
F2 = 160N F1 = 80N
VT
9 tháng 7 2018
Đáp án A
Ta có trọng lực của thanh P = m g = 24.10 = 240 ( N )
Gọi Lực tác dụng ở điểm A là P1 cách trọng tâm d1
Lực tác dụng ở điểm A là P2 cách trọng tâm d2
Vì F → 1 ; F → 2 cùng phương cùng chiều nên P= F1 + F2 = 240N ⇒ F1 = 240 – F2
Áp dụng công thức: F1.d1 = F2.d2 ⇒ ( 240 – F2).2,4 = 1,2.F2
⇒ F2 = 160N ⇒ F1 = 80N
VT
13 tháng 4 2017
Đáp án A
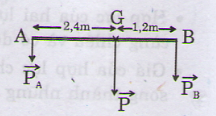
P = P1 + P2 = 240N → P1 = 240 – P2
P1.d1 = P2.d2 ↔ (240 – P2).2,4 = 1,2P2
↔ P2 = 160N → P1 = 80N.
15 tháng 12 2021
Gọi \(F_1;F_2\) lần lượt là các lực tác dụng lên bờ mương 1 và 2.
Theo quy tắc Momen lực ta có:
\(d_1\cdot F_1=d_2F_2\)
\(\Rightarrow2,4\cdot F_1=1,2\cdot F_2\left(1\right)\)
Mà \(F_1+F_2=240\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}F_1=80N\\F_2=160N\end{matrix}\right.\)
VT
10 tháng 4 2019
Đáp án C
Gọi F 1 , F 2 là độ lớn của hai lực đặt lên hai đầu điểm tựa A và B.
F 1 , F 2 lần lượt cách vai là d 1 = 60 cm, d 2 = 40 cm.
Ta có: F 1 + F 2 = 1000 (1)
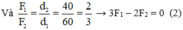
Từ (1) và (2) → F 1 = 400 N, F 2 = 600 N
16 tháng 4 2017
Tương tự bài 3. P = PA + PB = 240 (1)
PA. GA = PB.GB
=> PB = PA. = 2 PA (2)
(1) và (2) => P = 3 PA => PA == 80N
Chọn B
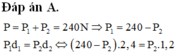
trọng lực của hỗn hợp kim loại P=m.g=240N
gọi lực tác dụng lên điểm A là P1
lực tác dụng lên điểm B là P2
hai lực này song song và cùng chiều nên P=P1+P2=240N\(\)\(\Rightarrow\)P1=240-P2 (1)
ta có P1.s1=P2.s2\(\Rightarrow\)P1.2,4=P2.1,2 (2)
từ (1),(2)\(\Rightarrow\)P2=160N\(\Rightarrow\)P1=80N
:))