Cho số 20a15b tìm các chữ số a,b để n chia hết cho cả 2,3,5 và 9.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VQ
20 tháng 8 2016
B1/
Không có giá trị * nào thỏa mãn 457* chia hét cho cả 2, 3, 5 và 9 vì:
- Để 457* chia hết cho 2 và 5 thì * phải bằng 0 (* phải cố định là 0)
- Mà 457* còn phải chia hết cho 3 và 9 mà số 4570 không chia hết cho 3 và 9
Vậy không có giá trị * thỏa mãn
B2/
a/ Để 3a78b chia hết cho 2 và 5 thì chữ số cuối phải bằng 0, tức b = 0
Để 3a780 chia hết cho 3 và 9 thì 3a780 phải chia hết cho 9
Mà 3 + a + 7 + 8 + 0 = 18 + a suy ra a = 0 hoặc a = 9
Vậy hai số tìm được là: 30780 hoặc 39780
b/ Để 4a5b chia hết cho 2 và 5 nên chữ số cuối tức b = 0
Để 4a50 chia hết cho 3 nhưng không chia hết cho 9 thì
4 + a + 5 + 0 = 9 + a chia hết cho 3 không chia hết cho 9
Suy ra a = 3 hoặc a = 6
Vậy hai số tìm được là 4350 hoặc 4650
NP
0
TV
4
DL
15 tháng 4 2017
a2008b chia hết cho 2 và 5
b=0
a20080 chia hết cho 3,9
a=8 ( 8+2+8=18 chia hết cho 3,9)
a2008b=820080
15 tháng 2 2023
Bài 9:
a) Ta thấy nếu như muốn chia hết cho 2 và 5 thì số tận cùng là 0. Vậy thay b bằng 0 để được số 24a0. Còn chia hết cho 3 và 9 thì a có thể là số 3.
b) 28320 hoặc 28350.
H9
HT.Phong (9A5)
CTVHS
1 tháng 11 2023
a) Để \(\overline{163a}\) chia hết cho 5 thì \(a\in\left\{0;5\right\}\)
Mà số đó lại chia hết cho 3 nên: \(1+6+3+a=10+a\) ⋮ 3
Với a = 0 thì 10 + 0 = 10 không chia hết cho 3 (loại)
Với a = 5 thì 10 + 5 = 15 ⋮ 3 (nhận)
Vậy a = 5
b) Để \(\overline{712a4b}\) chia hết cho 2 và 5 thì \(b=0\)
Số đó có dạng \(\overline{712a40}\)
Mà số đó lại chia hết cho 3 và 9 nên: \(7+1+2+a+4+0=14+a\) ⋮ 9
\(14+a=18\Rightarrow a=4\)
Vậy (a;b) = (4;0)
TK
4
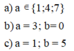
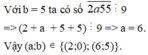
a=1 ; b=0
ta được số 201150
A = 1
B = 0