Cổng Arch được xem là đường Parabol, người ta đo khoảng cách giữa chân cổng là 162m. Từ một điểm trên thân cổng người ta đo được khoảnh cách tới mặt đất là 43m và khoảng cách tới chân cồng gần nhất là 44,15m. Hãy tính chiều cao cổng ? ( tính từ điểm cao nhất của cổng xuống mặt đất, làm tròn kết quả đến hàng đơn vị )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

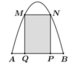
Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
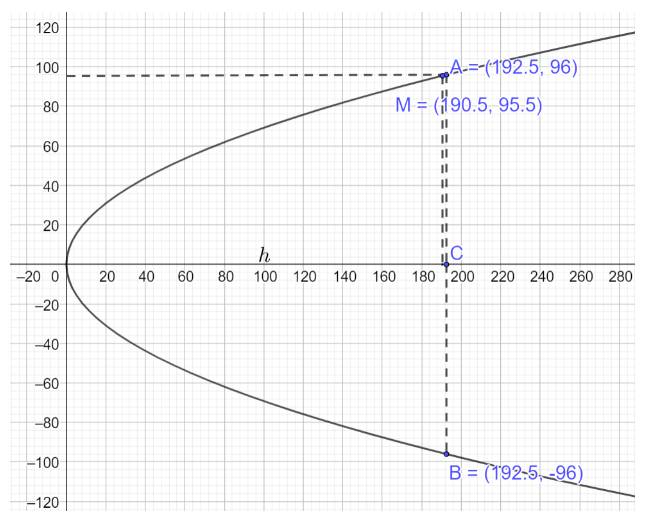
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m

Theo bài ra ta có:
AB=8m => AO=OB=4m
AC=0,5m => OC=OA-AC=3,5m
=> Parabol đi qua điểm A(-4;0); B(4;0); C(-3,5; 2,93)
Do đó ta có các phương trình sau:
\(a.{( - 4)^2} + b( - 4) + c = 0 \Leftrightarrow 16a - 4b + c = 0\)
\(a{.4^2} + 4b + c = 0 \Leftrightarrow 16a + 4b + c = 0\)
\(a.{( - 3,5)^2} + b( - 3,5) + c = 2,93 \Leftrightarrow 12,25a - 3,5b + c = 2,93\)
Từ 3 phương trình trên, ta có: \(a = \frac{{ - 293}}{{375}};b = 0;c = \frac{{4688}}{{375}}\)
Tọa độ đỉnh là \(I\left( {0;\frac{{4688}}{{375}}} \right)\)
Vậy chiều cao của cổng parabol là \(\frac{{4688}}{{375}} \approx 12,5m\)
=> Kết quả của An tính ra không chính xác.

Phương pháp:
+ Tìm phương trình Parabol
+ Diện tích hình phẳng giới hạn bởi
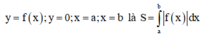
+ Tính diện tích hình chữ nhật từ đó tính diện tích phần trồng hoa và tính số tiền cần dùng để mua hoa trang trí.
Cách giải:
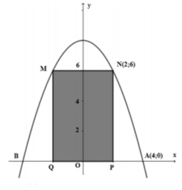
Gắn hệ trục tọa độ Oxy như hình vẽ, ta có Parabol đi qua các điểm A 4 ; 0 ; N 2 ; 6

Hoành độ giao điểm của Parabol và trục hoành là


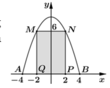
Chọn hệ trục tọa độ Oxy như hình vẽ.
Parabol đối xứng qua Oy nên có dạng ![]()
Vì (P) đi qua B(4;0) và N(2;6) nên ![]()
Diện tích hình phẳng giới hạn bởi (P) và trục Ox là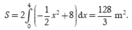
Diện tích phần trồng hoa là ![]()
Do đó số tiền cần dùng để mua hoa là ![]()
Chọn D.

Đặt hệ trục tọa độ Oxy vào cổng với gốc tọa độ trùng điểm chính giữa hai chân cổng
Gọi 2 chân cổng là A và B, điểm cao nhất là C, điểm có độ cao 43m là D
\(\Rightarrow A\left(-81;0\right)\) ; \(B\left(81;0\right)\); \(D\left(71;43\right)\)
Phương trình parabol có dạng \(y=ax^2+bx+c\)
Thay tọa độ A; B; C vào ta được hệ:
\(\left\{{}\begin{matrix}81^2.a-81b+c=0\\81^2a+81b+c=0\\71^2a+71b+c=43\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{43}{1520}\\b=0\\c=\frac{81^2.43}{1520}\end{matrix}\right.\)
\(\Rightarrow\) Độ cao cổng cũng là tung độ đỉnh C
\(\Rightarrow h=y_C=c\simeq185,6\left(m\right)\)