Cho hàm số y = f x , y = g x co cùng tập xac định D . Chứng minh rằng
a) nếu 2 ham số trên lẽ thi hàm số y = f x + g x la hàm số lẻ
b) nếu 2 hàm so tren mot chẵn mot lẽ thi ham so y = f x + g x là hàm số lẻ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 4 2018
Giả sử ( x n ) là dãy số bất kì thoả mãn n < a và x n → − ∞
Vì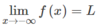 
nên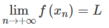 
Vì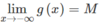 
nên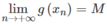 
Do đó,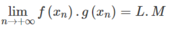 
Từ định nghĩa suy ra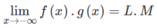 
CM
26 tháng 10 2019
Đặt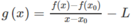 
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và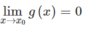 
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
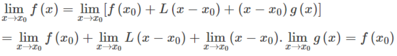
Vậy hàm số y = f(x) liên tục tại
8 tháng 2 2017
xét từng th
A(0;-2)=>0^2-2=0-2=-2=>A THUỘC HÀM SỐ Y=F(X)
B(-1;-3)=>-1^2-2=-1-2=-3=>B THUỘC HÀM SỐ Y=F(X)
C(1;-3)=>1^2-2=2-2=0=>C KO THUỘC HÀM SO Y=F(X)
=>NHỮNG ĐIỂM THUỘC H/S Y=F(X)LÀ ĐIỂM A(0;-2);B(-1;-3)
25 tháng 10 2021
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
27 tháng 12 2017
Ta có: f(-1)=3*(-1)-7=-3-7=-10
f(0)=3*0-7=0-7=-7
Vậy f(-1)=-10 ;f(0)=-7
Xét điểm M(2;-1) ta có
Với x=2 => y=3*2-7=-1
=> Điểm M(2;-1) thuộc đồ thị hàm số y=3x-7
Vậy điểm M(2;-1) thuộc đồ thị hàm số y=3x-7
Tích mk nha pn....
NT
27 tháng 12 2017
Ta có :y=f(x)=f(-1)=3*-1-7=-10
y=f(x)=f(0)=3*0-7=-7
M(2;-1)=>x=2;y=-1
=>y=3*2-7=-1
=>M thuộc hàm số y=3x-7
CM
4 tháng 2 2017
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
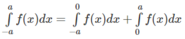
Đổi biến x = - t đối với tích phân
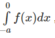
Ta được:
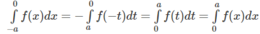
Vậy
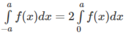
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì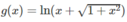 
là hàm số lẻ trên đoạn [-2; 2] nên 