Vẽ ba đường thẳng aa', bb' và cc' cắt nhau tại A. Hãy viết tên các cặp góc đối đỉnh (khác góc bẹt).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
7 tháng 10 2021
Tìm ra B1 đồng vị vs C1 và C1 nên b//c
A1 và C1 so le trong nên a//c
Mà b//c,c//a suy ra a//b .
Ok nha bạn
CM
23 tháng 5 2018
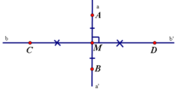
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
\(\widehat{aAb}=\widehat{a'Ab'};\widehat{bAc}=\widehat{b'Ac'};\widehat{cAa'}=\widehat{c'Aa};\widehat{aAc}=\widehat{a'Ac'};\widehat{a'Ab}=\widehat{aAb'};\widehat{cAb'}=\widehat{c'Ab}\)