Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy điểm C, D cách đều O. Từ C, D kẻ hai tia song song cắt nửa đường tròn ở C', D'. Chứng minh C'D' vuông góc CC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 9 2017
Hình bạn tự vẽ nhé!
Gọi I là trung điểm của DE.
Từ I dựng IH vuông góc với AB tại H.
Ta có: Ax//By
=> Tứ giác ABED là hình thang.
và ID = IE (I là trung điểm của DE)
OA = OB (O là tâm của đường tròn đường kính AB)
=> OI là đường trung bình của hinh thang ABED
=> OI//AD
=> SAOI = SDOI
=> 1/2.OA.IH = 1/2.DI.OC
Mà OI = OC
=> IH = DI = IE
Mà IH vuông góc với AB (cách lấy điểm H)
=> AB là tiếp tuyens của đường tròn đường kính DE.
CM
12 tháng 6 2018
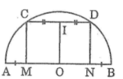
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.
Hình tự vẻ nha em
gợi ý, gọi O' là trung điểm của C'D'
dễ dàng cm được OO' là ĐTB của hình thanh CC'D'D. nên CC' ss DD' ss OO'
mặt khác, OO' là 1 phần đường kính qua trung điểm O' của dây cung C'D'
nên theo liên hệ ĐKDC thì OO' vuong goc C'D'
nên suy ra đpcm là CC' vuông góc với C'D'
chúc em học tập tốt em nhé