Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nhé!
Gọi I là trung điểm của DE.
Từ I dựng IH vuông góc với AB tại H.
Ta có: Ax//By
=> Tứ giác ABED là hình thang.
và ID = IE (I là trung điểm của DE)
OA = OB (O là tâm của đường tròn đường kính AB)
=> OI là đường trung bình của hinh thang ABED
=> OI//AD
=> SAOI = SDOI
=> 1/2.OA.IH = 1/2.DI.OC
Mà OI = OC
=> IH = DI = IE
Mà IH vuông góc với AB (cách lấy điểm H)
=> AB là tiếp tuyens của đường tròn đường kính DE.

Kẻ OI ⊥⊥ AB ( I ∈∈ CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có IO=CA+DB2 =MC+MD2 =DC2 là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.
Kẻ OI \bot⊥ AB ( I \in∈ CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có IO=\dfrac{CA+DB}{2}=\dfrac{MC+MD}{2}=\dfrac{DC}{2}IO=2CA+DB=2MC+MD=2DC là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.

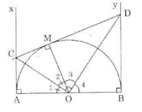
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)

Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)

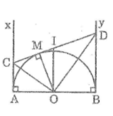
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
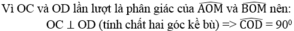
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

Bài 1:
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi
mong mọi giúp với ạ thank