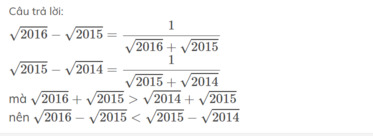tính \(\sqrt{2016}-\sqrt{2015}Và\sqrt{2015}-\sqrt{2014}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HA
2
13 tháng 1 2021
Ta có: \(\sqrt{2015}-\sqrt{2014}=\dfrac{2015-2014}{\sqrt{2015}+\sqrt{2014}}>\dfrac{2016-2015}{\sqrt{2016}+\sqrt{2015}}=\sqrt{2016}-\sqrt{2015}\)
HN
13 tháng 1 2021
Ta có: √2015−√2014=2015−2014√2015+√2014>2016−2015√2016+√2015=√2016−√2015
TT
1
5 tháng 2 2022
\(\sqrt{2016}-\sqrt{2015}=\dfrac{1}{\sqrt{2016}+\sqrt{2015}}\)
\(\sqrt{2015}-\sqrt{2014}=\dfrac{1}{\sqrt{2015}+\sqrt{2014}}\)
mà \(\sqrt{2016}+\sqrt{2015}>\sqrt{2014}+\sqrt{2015}\)
nên \(\sqrt{2016}-\sqrt{2015}< \sqrt{2015}-\sqrt{2014}\)
27 tháng 7 2017
Ta có:
\(\frac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\frac{1}{\sqrt{n\left(n+1\right)}\left(\sqrt{n+1}+\sqrt{n}\right)}\)
\(=\frac{\left(\sqrt{n+1}-\sqrt{n}\right)}{\sqrt{n\left(n+1\right)}}=\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\)
Thế vô bài toán được
\(\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+...+\frac{1}{2016\sqrt{2015}+2015\sqrt{2016}}\)
\(=\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2015}}-\frac{1}{\sqrt{2016}}\)
\(=1-\frac{1}{\sqrt{2016}}\)
PK
1
30 tháng 10 2016
Áp dụng bđt \(\frac{\sqrt{a}+\sqrt{b}}{2}< \sqrt{\frac{a+b}{2}}\) với a > 0; b > 0; a \(\ne\) b ta có:
\(\frac{\sqrt{2016}+\sqrt{2014}}{2}< \sqrt{\frac{2016+2014}{2}}\)
\(\Rightarrow\frac{\sqrt{2016}+\sqrt{2014}}{2}< \sqrt{\frac{4030}{2}}\)
\(\Rightarrow\frac{\sqrt{2016}+\sqrt{2014}}{2}< \sqrt{2015}\)
\(\Rightarrow\sqrt{2016}+\sqrt{2014}< 2.\sqrt{2015}\)
\(\Rightarrow\sqrt{2016}-\sqrt{2015}< \sqrt{2015}-\sqrt{2014}\)
TT
1
LA
1
PT
1
19 tháng 10 2015
\(\sqrt{2016}+\sqrt{2015}>\sqrt{2015}+\sqrt{2014}\)
=> \(\frac{1}{\sqrt{2016}+\sqrt{2015}}