Trên cạnh AC của tam giác ABC lấy điểm D kéo dài CB đén E sao cho BE=AD,ED và AB cắt nhau tại F.Chứng minh rằng \(\dfrac{EF}{FD}=\dfrac{AC}{BC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 3 2021
a) Xét ΔDAB và ΔDEB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔDAB=ΔDEB(c-g-c)
Suy ra: DA=DE(Hai cạnh tương ứng)
7 tháng 3 2022
a: Ta có: AE+BE=AB
AF+FC=AC
mà AB=AC
và BE=FC
nên AE=AF
hay ΔAEF cân tại A
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
=>\(\widehat{AEF}=\widehat{ABC}=\widehat{ACB}\)
5 tháng 3 2022
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
d: Ta có: DK=DC
mà DC>DE
nên DK>DE
10 tháng 6 2020
a. Ta có: \(\frac{AB}{AC}=\frac{4,8}{6,4}=\frac{3}{4}\\ \frac{AE}{AD}=\frac{2,4}{3,2}=\frac{3}{4}\)
suy ra \(\frac{AB}{AC}=\frac{AE}{AD}\)
xét 2 tam giác ABC và AED có:
góc A chung
\(\frac{AB}{AC}=\frac{AE}{AD}\)(c/m trên)
suy ra 2 tam giác đồng dạng suy ra \(\widehat{ACB}=\widehat{ECF}=\widehat{ADE}\)
b. \(\widehat{ADE}=\widehat{BDF}\)(đối đỉnh) \(\Rightarrow\widehat{BDF}=\widehat{ECF}\)
xét 2 tam giác FDB và FCE có:
góc F chung
góc BDF = góc ECF (c/m trên)
suy ra 2 tam giác đồng dạng (g.g)
\(\Rightarrow\frac{FB}{FE}=\frac{FD}{FC}=\frac{DB}{CE}\)
c. BD=AB-AD=4,8-3,2=1,6
CE= AC-AE = 6,4-2,4 =4
khi đó:
\(\frac{FB}{FE}=\frac{FD}{FC}=\frac{1,6}{4}=\frac{2}{5}\Leftrightarrow\frac{FB}{FD+1,8}=\frac{FD}{FB+3,6}=\frac{2}{5}\)
suy ra hpt: \(\hept{\begin{cases}5FB=2FD+3,6\\5FD=2FB+7,2\end{cases}}\Leftrightarrow\hept{\begin{cases}5FB-2FD=3,6\\2FB-5FD=-7,2\end{cases}}\Leftrightarrow\hept{\begin{cases}FB=\frac{54}{35}\\FD=\frac{72}{35}\end{cases}}\)
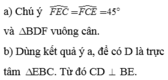
Kẻ DH // AB (\(H\in BC\))
Vì \(\Delta ABC\) có DH // AB nên theo định lí Ta-lét ta có:
\(\dfrac{AC}{AD}=\dfrac{BC}{BH}\Leftrightarrow\dfrac{AC}{BC}=\dfrac{AD}{BH}\Leftrightarrow\dfrac{AC}{BC}=\dfrac{EB}{BH}\) (1) (Vì AD = EB)
Trong tam giác EDH có BF // DH (vì AB // DH) nên theo định lí Ta-lét ta có: \(\dfrac{EB}{BH}=\dfrac{EF}{FD}\) (2)
Từ (1), (2) suy ra: \(\dfrac{AC}{BC}=\dfrac{EF}{FD}\)