Nêu các bước vẽ hình bình hành ABCD bằng Geogebra
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
20 tháng 8 2023
Xét hình bình hành ABCD có:
\(AB=CD=8\left(cm\right)\)
Đặt độ dài cạnh BC của hình bình hành là x:
\(BC=AD=x\left(cm\right)\)
Chu vi hình bình hành là 30cm:
\(2AB+2BC=30\left(cm\right)\\ \Leftrightarrow2.8+2BC=30\\ \Leftrightarrow BC=\dfrac{30-16}{2}=7\left(cm\right)\)
3 tháng 5 2018
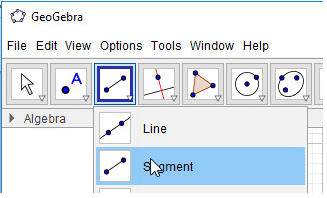
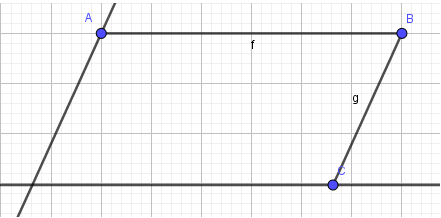
1. Vẽ hai cạnh AB và BC:
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng
:
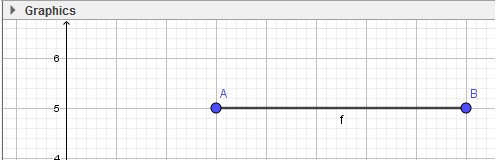
- Bước 2: Nháy chuột tại vị trí trống bất kì trên màn hình (em sẽ thấy xuất hiện điểm A), di chuyển đến vị trí thứ hai và nháy chuột. Như vậy ta vừa tạo xong đoạn AB.
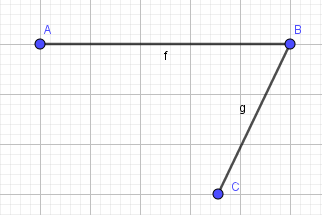
- Bước 3: Tạo cạnh BC bằng cách tương tự như AB:
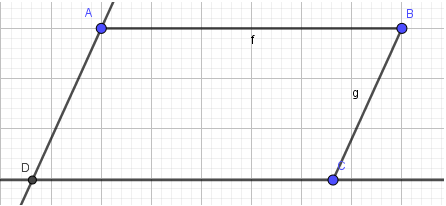
2. Vẽ điểm D và 2 cạnh còn lại
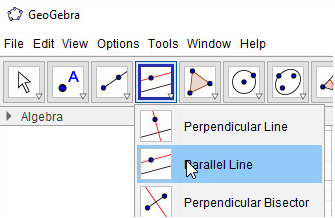
- Bước 1: Nháy chuột chọn công cụ Đường song song
:
- Bước 2: Chọn điểm, sau đó chọn đoạn thẳng để vẽ đường thẳng song song:
Bước 3: Đánh dấu giao điểm của 2 đường thẳng vừa tạo là điểm D:
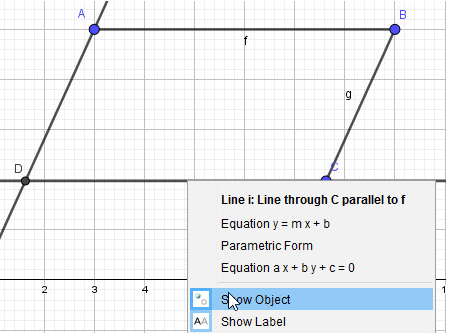
- Bước 4: Ẩn các đối tượng đường song song vừa tạo:
Lần lượt nhấn chuột phải vào các đường thẳng song song vừa tạo và chọn Hiển thị đối tượng (Show Object):
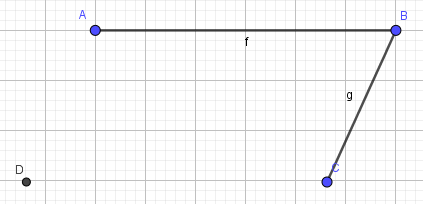
→ Kết quả:
- Bước 5: Sử dụng công cụ Đoạn thẳng để vẽ hai cạnh còn lại là AD và CD. Như vậy em đã vẽ xong được hình bình hành ABCD.
chúc bn học tốt
CM
3 tháng 11 2017
Cách 1:
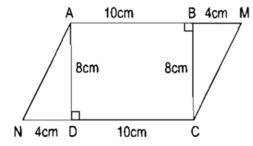
Nhìn hình ta có: AD = BC = 8cm; BM = ND = 4cm
nên diện tích tam giác AND = diện tích tam giác BMC.
Diện tích tam giác AND là:
4 × 8 : 2 = 16 ( c m 2 )
Diện tích hình chữ nhật ABCD là
10 × 8 = 80 ( c m 2 )
Diện tích hình bình hành AMCN là:
Diện tích hình chữ nhật ABCD + diện tích tam giác AND + diện tích tam giác BCM = 80 + 16 + 16 = 112 (cm2)
Cách 2:
Nối hai điểm AC ta được 2 tam giác bằng nahu CAN = ACM
Với NC = AM = 14cm là hai cạnh đáy của 2 tam giác trên
Diện tích tam giác CAN là:
14 × 8 : 2 = 56 ( c m 2 )
Diện tích hình bình hành AMCN là:
56 × 2 =112 ( c m 2 )
TM
2
11 tháng 10 2021
Bước 1. Vẽ đoạn thẳng AB = 6 cm.
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
11 tháng 10 2021
TL
Lời giải:
Vẽ hình chữ nhật ABCD có một cạnh bằng 6 cm, một cạnh bằng 4 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 6 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 4 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 4 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
HT
14 tháng 3 2020
Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
⇒⇒FG//ADFG//AD
C/m tương tự đc EH//AD;GH//EF//BCEH//AD;GH//EF//BC
⇒EFGH⇒EFGH là hình bình hành
a/Để EFGH là hình chữ nhật thì góc FGH=90oFGH=90o
⇒gócHGD+gócFGC=90o⇒gócHGD+gócFGC=90o
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
⇒⇒ góc BCD+góc ADC=90o90o
⇒⇒Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=90o90o
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
⇒⇒AD=BC
⇒⇒Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi⇒⇒ABCD phải có đủ cả hai điều kiện trên
14 tháng 3 2020
Nối A với C ta có AP là đường trung tuyến của ΔACDΔACD nên
SADP=SAPC=12SADC=14SABCDSADP=SAPC=12SADC=14SABCD
Tương tự SACR=SBCR=12SABC=14SABCD.SACR=SBCR=12SABC=14SABCD.
⇒SAPC+SACR=SARCP=12SABCD.⇒SAPC+SACR=SARCP=12SABCD.
SADP=SAPC=12SADC=14SABCDSADP=SAPC=12SADC=14SABCD
Tương tự SACR=SBCR=12SABC=14SABCD.SACR=SBCR=12SABC=14SABCD.
⇒SAPC+SACR=SARCP=12SABCD.⇒SAPC+SACR=SARCP=12SABCD.
Gọi H là giao điểm của AP và BQ, K là giao điểm của CR và BQ, M là giao điểm của AP và DS, N là giao điểm của CR và DS.
Dễ thấy HKNM là hình bình hành nên các tam giác sau đây có cùng diện tích:
SAKH=SHKM=SMNH=SMNCSAKH=SHKM=SMNH=SMNC=SAKB=SMCD=SAKB=SMCD
Mà SAKR=12SAKBSAKR=12SAKB (đáy gấp đôi, chung đường cao)
Tương tự SMPC=12SMCDSMPC=12SMCD
⇒SAKH=SHKM=SMNH⇒SAKH=SHKM=SMNH=SMNC=(SAKR+SMPC)=SMNC=(SAKR+SMPC)=15SARCP.=15SARCP.
Mà SARCP=12SABCDSARCP=12SABCD
⇒SHKM+SMKN=15SABCD⇒SHKM+SMKN=15SABCD hay SKHMN=15SABCD.