1. Mình và Năm đứng ở hai điểm M, N cách nhau 750m trên một bãi sông. Khoảng cách từ M đến sông là 150m, từ N đến sông là 600m. Tính thời gian ngắn nhất để Mình chạy ra sông múc thùng nước mang đến ch...

TM

Tattoo mà ST vẽ lên thôi

20 tháng 2 2018

1. Mình và Năm đứng ở hai điểm M, N cách nhau 750m trên một bãi sông. Khoảng cách từ M đến sông là 150m, từ N đến sông là 600m. Tính thời gian ngắn nhất để Mình chạy ra sông múc thùng nước mang đến chỗ Nam. Cho biết đoạn sông thẳng, vận tốc chạy của Minh không không đổi V=2m/s, bỏ qua thời gian múc...

Đọc tiếp

#Vật lý lớp 8

1

TL

Team lớp A

20 tháng 2 2018

Cơ học lớp 8

Đúng(2)

NC

Nguyễn Cúnn

19 tháng 11 2019

sơ đồ như thế nào ạ

Đúng(0)

WR

wary reus

25 tháng 7 2016

Mnh và Nam đứng ở hai đểm M , N cách nhau 750m trên một bãi sông. Khoảng cách từ M đến sông 150m từ N đến sông 600m. Tính thời gan ngắn nhất để Minh hạy ra sông múc một thùng nước mang đến chỗ Nam . Cho biết đoạn sông thẳng , vận tốc chạy của Minh không đổi v= 2m/s , bỏ qua thời gian múc nước

#Vật lý lớp 8

3

VD

Võ Đông Anh Tuấn

25 tháng 7 2016

thoi gian nguoi do di nua duong dau
t1=s1/v1
ma s1=s2=s/2(nua duong)
=>t1=s/(2v1)
thoi gian di nua duong sau
t2=s/(2v2)
tong thoi gian di la
t=t1+t2=s/2(1/v1+1/v2)
=s(v1+v2)/(2v1v2)
van toc trung binh la quang duong chia thoi gian
vtb=s/t
=2v1v2/(v1+v2)
thay so vao
vtb=14,4km/h=4m/s

Đúng(0)

LN

Lê Nguyên Hạo

25 tháng 7 2016

Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.

Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'

Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'

=> NP = NK - PK = NK - NH = 450 (m)

\(MP=\sqrt{MN^2-NP^2}=600\left(m\right)\)

N'P = N'K + KP = 750 (m)

MN' = \(\sqrt{MP^2+N'P^2}=150\sqrt{41m}\)

Thời gian ngắn nhất là :

\(t=\frac{MN'}{V}=\frac{150\sqrt{41}}{2}=75\sqrt{41}=480\left(s\right)=8ph\text{út}\)

Đúng(0)

NT

Nguyễn Tiến Đức

21 tháng 10 2018 - olm

Minh và Nam đứng ở hai đểm M , N cách nhau 750m trên một bãi sông. Khoảng cách từ M đến sông 150m từ N đến sông 600m. Tính thời gan ngắn nhất để Minh hạy ra sông múc một thùng nước mang đến chỗ Nam . Cho biết đoạn sông thẳng , vận tốc chạy của Minh không đổi v= 2m/s , bỏ qua thời gian múc nước

vẽ sơ đồ chuyển động

#Toán lớp 8

2

HT

Hoàng Thế Hải

21 tháng 10 2018

Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.

Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'

Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'

=> NP = NK - PK = NK - NH = 450 (m)

\(MP=\sqrt{MN^2-NP^2}=600\left(m\right)\)

N'P = N'K + KP = 750 (m)

\(MN'=\sqrt{MP^2+N'P^2}=150\sqrt{41}\left(m\right)\)

Thời gian ngắn nhất là :

\(t=\frac{MN'}{V}=\frac{150\sqrt{41}}{2}=75\sqrt{41}=480\left(s\right)=8\left(phút\right)\)

Đúng(0)

HT

Hoàng Thế Hải

21 tháng 10 2018

Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.

Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'

Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'

=> NP = NK - PK = NK - NH = 450 (m)

MP=√MN2−NP2=600(m)

N'P = N'K + KP = 750 (m)

MN'=√MP2+N'P2=150√41(m)

Thời gian ngắn nhất là :

t=MN'V =150√412 =75√41=480(s)=8(phút)

Đúng(0)

LD

Lưu Đức Mạnh

18 tháng 7 2017 - olm

Minh và Nam đứng ở hai điểm MN cách nhau 750m. Trên một con sông, khoảng cách từ M đến sông là 150m và từ N đến sông là 600m. Tính thời gian ít nhất để Minh chạy ra sông lấy một thùng nước mang đến chỗ Nam. Biết con sông thẳng và vận tốc của Minh là 2m/s.

#Toán lớp 8

0

PT

Pham Trong Bach

2 tháng 3 2019

Cho hai vị trí A, B cách nhau 615m, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118m và 487m. Một người đi từ A đến bờ sông để lấy nước mang về B. Đoạn đường ngắn nhất mà người đó có thể đi là A. 810,3m B. 807,5m C. 779,8m D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

2 tháng 3 2019

Chọn đáp án C

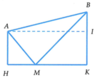
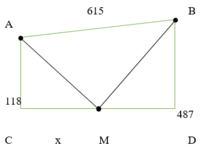
Khoảng cách từ A đến bờ sông là A H = 118 m ; khoảng cách từ B đến bờ sông là B K = 487 m (hình vẽ).

ta có

⇒ H K = 492 m .

Người đó đi từ A đến vị trí M trên bờ sông để lấy nước, sau đó mang về B.

Đoạn đường người đó đi được là

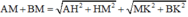
Đạo hàm

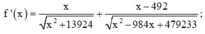
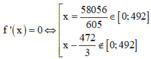
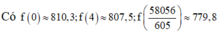
Vậy đoạn đường ngắn nhất người đó có thể đi là ≈ 779 , 8 m

Đúng(2)

NH

Nguyễn Hoàn Đại Ngọc

18 tháng 10 2018 - olm

Hai người đứng ở một bên bờ sông cách nhau 250m cùng nhìn thấy một cù lao trên sông với các góc nâng lần lượt là 30 độ và 40 độ. Tính khoảng cách d từ bờ sông đến cù lao. (Vẽ thành hình tam giác. BC là bờ sông , AH là khoảng cách từ bờ sông đến cù lao)

#Toán lớp 9

0

PT

Pham Trong Bach

15 tháng 7 2019

Cho hai vị trí A, B cách nhau 615m, cùng nằm về một phía bờ song như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118m và 478m . Một người đi từ A đến bờ sông để lấy nước mang về B . Đoạn đường ngắn nhất mà người đó có thể đi là A. 569,5m. B. 671, 4 m. C. 779,8m. D. 741, 2...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

15 tháng 7 2019

Đáp án C

Cách 1: Giải bằng hàm số

Đặt CM = x (x > 0)

Dễ tính ra CD

Từ đề bài ta có: f (x) =

Quãng đường ngắn nhất người đó có thể đi

⇔ Giá trị nhỏ nhất của f(x) trên (0;492)

Ta có: f’(x) =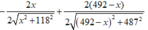

=> f’(x) = 0

Ta có bảng biến thiên

x

0

492

y’

+ 0 -

y

779,8

Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8

Cách 2: Giải bằng hình học

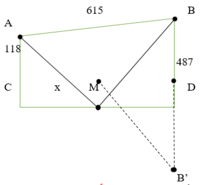
Gọi B’ là điểm đối xứng của B qua D

Dễ thấy AM + MB = AM + MB’

⇔ AM + MB ngắn nhất

⇔ AM + MB’ ngắn nhất

Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’

⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’

Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng

Đúng(0)

ND

Nông Đức Sếu

29 tháng 9 2017 - olm

nước của một dòng sông chảy với vận tốc 6km/ h 1 ca nô khii đi xuôi dòng sông từ điểm m đến điểm n mất khoảng thời gian chỉ bằng 1/3 thời gian khi đi ngược dòng hãy xác định vận tốc của ca nô nếu nó chạy ở trên mặt hồ nơi nước lặng và vận tốc trung bình từ m đến n rồi trở lại m

#Toán lớp 8

0