Cho tứ giác ABCD. Vẽ các hình bình hành ABID, ACJD. Chứng minh tứ giác BIJC là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2B
2
25 tháng 10 2021
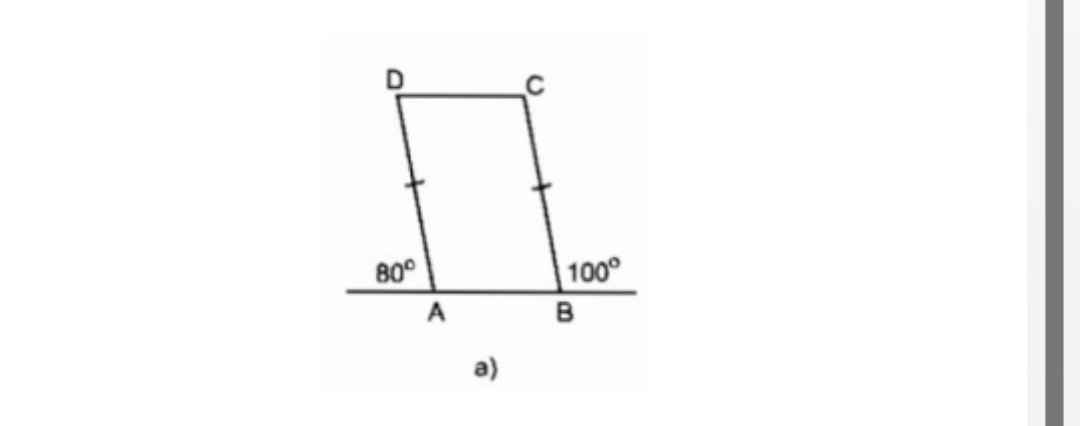
Ta có: \(\widehat{DAB}=180^0-80^0=100^0\)
\(\Rightarrow\widehat{DAB}=\widehat{B}=100^0\)
Mà 2 góc này đồng vị
=> AD//BC
Mà AD=BC
=> ABCD là hình bình hành
25 tháng 10 2021
Ta có \(\widehat{CAB}=180^0-80^0=100^0\left(kề.bù\right)=\widehat{B}\) mà 2 góc này ở vị trí đồng vị nên AD//BC
Mà \(AD=BC\) nên ABCD là hbh
.
19 tháng 8 2021
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
27 tháng 10 2021
b: Xét tứ giác EBFD có
ED//BF
ED=BF
Do đó: EBFD là hình bình hành
19 tháng 7 2017
a) xét tg AECF có : AF//EC (vì AB//CD, tgABCD là hbh)
và AE//CF ( cùng ^ vsBD)
=> tgAECF là hbh
b)xét tg AMD và tg CNB có:
AD=BC (tgABCD là hbh)
AMD =CNB =90
ADM =CBN (AD//BC)
=>tg AMD =tg CNB (ch-gn)
=>AM=CN (2 cạnh t/ư )
xét tg AMCN có: AM//CN (do cùng ^ BD) và AM =CN (cmt)
==>tg AMCN là hbh
2 tháng 9 2016
Lấy E là trung điểm A'D ; F là trung điểm BC'.
Dễ dàng chứng minh được \(\Delta EQM=\Delta FNP\left(c.g.c\right)\)
Từ đó suy ra \(MQ=NP\)
CMTT có \(MN=PQ\)
Do đó \(MNPQ\)là hình bình hành.
Vậy ...
16 tháng 9 2023
a: góc ABM=góc MBC
góc MBC=góc AMB
=>góc ABM=góc AMB
=>ΔABM cân tại A
b: Xét ΔBAM và ΔDCN có
góc ABM=góc CDN
BA=DC
góc A=góc C
Do đó: ΔBAM=ΔDCN
=>AM=CN
AM+MD=AD
BN+NC=BC
mà AD=BC và AM=CN
nên MD=BN
Xét tứ giác MDNB có
MD//NB
MD=NB
Do đó: MDNB là hình bình hành
ta có hbh ABID => AD=BI; AD//BI
ta có hbh ACJD=> AD//CJ; AD=CJ
=> BI//CJ( // AD); BI=CJ (=AD)
=> BICJ là hbh
sửa lại là: BIJC là hbh nhé