cho tam giác ABC cân ai A,M là trung điểm của cạnh BC và B=40do
a, vẽ hình ghi giả thiết kết luận
b, chứng minh rằng : tam giác AMB=tam giacAMC
c, hoi goc BAM bang bao nhieu?vi sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GT : \(\Delta ABC\); AB = AC ; BM = MC ( M \(\in\)BC ) ; \(\widehat{B}=40^o\)
KL : b) \(\Delta AMB=\Delta AMC\)
c) \(\widehat{BAM}=?\)
giải
b) vì \(\Delta ABC\)cân tại A nên AB = AC
M là trung điểm của BC nên BM = MC = \(\frac{BC}{2}\)
Xét \(\Delta AMB\)và \(\Delta AMC\)có :
AB = AC ( gt )
BM = MC ( gt )
AM ( cạnh chung )
Suy ra : \(\Delta AMB\)= \(\Delta AMC\)( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)( 2 góc tương ứng )
c) vì \(\Delta ABC\)cân tại A nên \(\widehat{B}=\widehat{C}=40^o\)
\(\Rightarrow\widehat{BAC}=180^o-\left(40^o+40^o\right)=100^o\)
Mà \(\widehat{BAC}=\widehat{BAM}+\widehat{CAM}\)
\(\Rightarrow\widehat{BAM}=\frac{100^o}{2}=50^o\)
vì tg ABC cân ở a=> góc B= gócC=40độ
b) * Xét tg AMB và tg AMC
+)AB=AC(Vì tg ABC cân ở A)
+) gócB= gócC (cmt)
+)BM=MC (vì M là trg điểm của BC)
=>tgAMB=tgAMC (CGC)
c)*Xét tg ABC :BAC+B+C=180độ
<=>BAC+40độ+40độ=180độ
=>BAC=100độ (1)
lại có tgAMB=tgAMC (cmt)
=>góc BAM=gócMAC (2)
Từ(1),(2)=>Góc BAM=góc MAC=100:2=50độ
=>góc BAM=50 độ (đpcm)

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
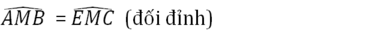
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


a:
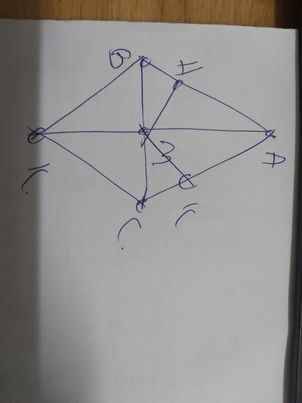
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M

| GT | ΔABC cân tại A, M là trung điểm của BC \(D\in\)AB DE\(\perp\)MA(E\(\in\)AC) |
| KL | a: ΔAMB=ΔAMC b: ΔADE cân |
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔAMB=ΔAMC
=>\(\widehat{BAM}=\widehat{CAM}\)
=>\(\widehat{DAM}=\widehat{EAM}\)
=>AM là phân giác của góc DAE
Xét ΔADE có
AM là đường cao
AM là đường phân giác
Do đó: ΔADE cân tại A

b: Ta có: ΔAIE cân tại A
mà AK là đường phân giác
nên K là trung điểm của EI
hay KE=KI
c: Xét ΔAID và ΔAED có
AI=AE
\(\widehat{IAD}=\widehat{EAD}\)
AD chung
Do đó: ΔAID=ΔAED
Suy ra: \(\widehat{AID}=\widehat{AED}=90^0\)
=>DE⊥AB
mà AC⊥AB
nên DE//AC
a. GT, KL tự ghi
b. Xét \(\Delta ABM,\Delta ACM\) có :
\(\left\{{}\begin{matrix}AB=AC\\AMchung\\MB=MC\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)\)
c, \(\Delta ABM=\Delta ACM\left(cmt\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=\widehat{C}\\\widehat{A1}=\widehat{A2}\end{matrix}\right.\)
Mà \(\widehat{B}=40^0\Leftrightarrow\widehat{C}=40^0\)
\(\Leftrightarrow\widehat{BAC}=180^0-40^0.2=100^0\) (định lí tổng 3 góc của tam giác)
\(\widehat{A1}=\widehat{A2}\left(cmt\right)\)
Lại có : \(\widehat{A1}+\widehat{A2}=\widehat{BAC}\)
\(\Leftrightarrow\widehat{A1}=\widehat{A2}=\dfrac{100^0}{2}=50^0\)