Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. GT, KL tự ghi
b. Xét \(\Delta ABM,\Delta ACM\) có :
\(\left\{{}\begin{matrix}AB=AC\\AMchung\\MB=MC\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)\)
c, \(\Delta ABM=\Delta ACM\left(cmt\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=\widehat{C}\\\widehat{A1}=\widehat{A2}\end{matrix}\right.\)
Mà \(\widehat{B}=40^0\Leftrightarrow\widehat{C}=40^0\)
\(\Leftrightarrow\widehat{BAC}=180^0-40^0.2=100^0\) (định lí tổng 3 góc của tam giác)
\(\widehat{A1}=\widehat{A2}\left(cmt\right)\)
Lại có : \(\widehat{A1}+\widehat{A2}=\widehat{BAC}\)
\(\Leftrightarrow\widehat{A1}=\widehat{A2}=\dfrac{100^0}{2}=50^0\)
b: Xét ΔMPE và ΔMQE có
MP=MQ
PE=QE
ME chung
Do đó: ΔMPE=ΔMQE
a: Xét ΔACI và ΔMCI có
CA=CM
ˆACI=ˆMCIACI^=MCI^
Do đó: ΔACI=ΔMC
5) Tam giác AMB và tam giác EMC có
- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
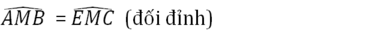
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)
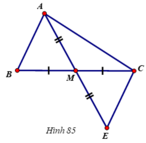
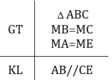
GT : \(\Delta ABC\); AB = AC ; BM = MC ( M \(\in\)BC ) ; \(\widehat{B}=40^o\)
KL : b) \(\Delta AMB=\Delta AMC\)
c) \(\widehat{BAM}=?\)
giải
b) vì \(\Delta ABC\)cân tại A nên AB = AC
M là trung điểm của BC nên BM = MC = \(\frac{BC}{2}\)
Xét \(\Delta AMB\)và \(\Delta AMC\)có :
AB = AC ( gt )
BM = MC ( gt )
AM ( cạnh chung )
Suy ra : \(\Delta AMB\)= \(\Delta AMC\)( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)( 2 góc tương ứng )
c) vì \(\Delta ABC\)cân tại A nên \(\widehat{B}=\widehat{C}=40^o\)
\(\Rightarrow\widehat{BAC}=180^o-\left(40^o+40^o\right)=100^o\)
Mà \(\widehat{BAC}=\widehat{BAM}+\widehat{CAM}\)
\(\Rightarrow\widehat{BAM}=\frac{100^o}{2}=50^o\)
vì tg ABC cân ở a=> góc B= gócC=40độ
b) * Xét tg AMB và tg AMC
+)AB=AC(Vì tg ABC cân ở A)
+) gócB= gócC (cmt)
+)BM=MC (vì M là trg điểm của BC)
=>tgAMB=tgAMC (CGC)
c)*Xét tg ABC :BAC+B+C=180độ
<=>BAC+40độ+40độ=180độ
=>BAC=100độ (1)
lại có tgAMB=tgAMC (cmt)
=>góc BAM=gócMAC (2)
Từ(1),(2)=>Góc BAM=góc MAC=100:2=50độ
=>góc BAM=50 độ (đpcm)