Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

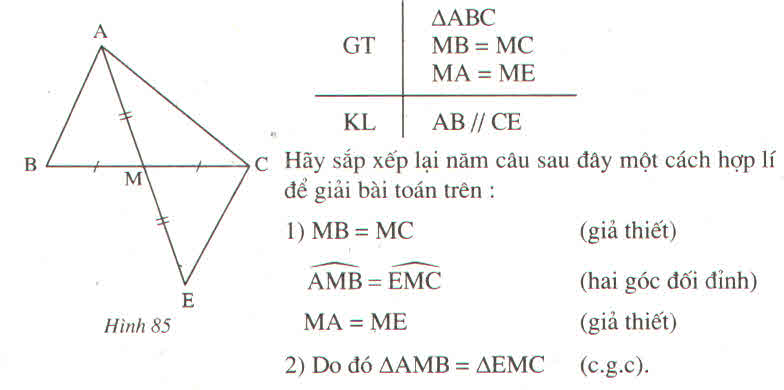
Xét tam giác ABM và tam giác MCE có
- BM = MC (Vì M là trung điểm BC)
-ME = MA ( giả thiết )
- góc BMA = góc CME (đối đỉnh)
Vậy tam giác ABM = tam giác MCE
=> góc BAM = góc CEM
=> AB//CE
Xét Δ ABM và Δ ECM có:
ME=MA ( theo giả thiết )
góc BMA= góc CME (đối đỉnh )
BM=CM ( do M là trung điểm của BC )
→ Δ ABM=Δ ECM ( C-G-C)
→ góc BAM= góc CEM
Mà 2 góc này ở vị trí so le trong nên AB //CE.

Bạn tự vẽ hình nhé !
Xét \(\Delta AMB\)và \(\Delta ECM\)có:
\(MA=ME\left(gt\right)\)
\(MB=MC\)( vì M là trung điểm BC )
\(\widehat{BMA}=\widehat{EMC}\)( 2 góc đối đỉnh )
\(\Rightarrow\Delta AMB=\Delta ECM\left(c.g.c\right)\)
Vì \(\Delta AMB=\Delta ECM\left(cmt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{MEC}\)( 2 góc tưởng ứng )
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CE\)
\(\text{a) xét tam giác AMB và tam giác EMC}\)
\(\text{có : MB=MC( M là trung điểm của BC)}\)
\(\text{góc AMB=góc EMC( đ đ)}\)
\(\text{AM=EM(gt)}\)
=> tam giác AMB=tam giác EMC(c-g-c)
\(\text{b) xét tam giác AMB và tam giác CME}\)
\(\text{có: AM=EM(gt)}\)
\(\text{góc AMB=góc CME (đ đ)}\)
\(\text{MB=MC(M là trung điểm của BC)}\)
=> tam giác AMB=tam giác CME(c-g-c)
=> góc CAM= góc MEC ( 2 góc tương ứng)
\(\text{mà 2 góc này ở vị trí so le trong}\)
=> AC=CE ( 2 cạnh tương ứng)

A B C H M F E I K
, M là trung điểm của BC ⇒ MB = MC
Xét ΔMBA và ΔMCE có:
MB = MC
\(\widehat{AMB}=\widehat{EMC}\)(đối đỉnh)
MA = ME
=> ΔMBA = ΔMCE (c.g.c) (đpcm)
b, Xét 2 tam giác vuông ΔBHA và ΔBHF có:
BH chung; \(\widehat{ABH}=\widehat{FBH}\) (do góc ABx nhận BC là tia phân giác)
=> ΔBHA = ΔBHF (cạnh góc vuông - góc nhọn)
=> AB = BF mà AB = CE (do ΔMBA = ΔMCE)
=> CE = BF (đpcm)
c, Ta thấy: \(\widehat{FBC}=\widehat{ABC}=\widehat{ECB}\)
=> ΔKBC cân tại K mà KM là trung tuyến
=> KM là phân giác của \(\widehat{BKC}\) (1)
ΔKBC cân tại K ⇒ KB = KC mà BF = CE
⇒ KB - BF = KC - CE ⇒ KF = KE
Ta chứng minh được ΔBEK = ΔCFK (c.g.c)
=> \(\widehat{EBK}=\widehat{FCK}\)
=.> ΔBIF = ΔCIE (g.c.g)
=> IF = IE ⇒ ΔIFK = ΔIEK (c.c.c)
\(\Rightarrow\widehat{IKF}=\widehat{IKF}\)
⇒ KI là phân giác của ^BKC (2)
Từ (1) và (2) suy ra M, I, K thẳng hàng (đpcm)

a/ Trong TG ABC : AB2=BC2-AC2 (đ/l Pytago đảo)
AB2=102-82=62
=> TG ABC là TG vuông .

b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC

A B C D E
GT KL tam giác ABC vuông tại A CA = CD CE = CB a, tam giác ABC = tam giác DEC b, tính góc CDE = 90 độ c. tính cạnh AB
a, Xét △ABC và △DCE có
AC = CD
C^ đối đỉnh
BC = CE
=> △ABC = △DCE
b, VÌ △ABC = △DCE nên góc BAC = góc CDE
=> CDE = 90 độ
c, Vì BE = BC + CE = 20
Mà BC = CE = \(\dfrac{BC}{2}\) = \(\dfrac{20}{2}\) = 10
Vì AD = AC + CD = 16
Mà AC = CD = \(\dfrac{AD}{2}\) = \(\dfrac{16}{2}\) = 8
Áp dụng định lý Pytago
ta có : \(BC^2=AB^2+AC^2\)
\(10^2=AB^2+8^2\)
\(100=AB^2+64\)
\(AB^2=100-64=36\)
Vậy \(AB=6^2\)
Mong bạn tick cho mik :))

a, tam giác ABC vuông tại A (gt) => BC^2 = AC^2 + AB^2 (pytago)
BC = 10; AB = 8 (Gt)
=> AC^2 = 10^2 - 8^2
=> AC^2 = 36
=> AC = 6 do AC > 0
b, xét tam giác AMB và tam giác DMC có : AM = MD (gt)
BM = MC do M là trung điểm của BC(gt)
^BMA = ^DMC (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
=> ^ABM = ^MCD mà 2 góc này slt
=> AB // CD
AB _|_ AC
=> CD _|_ AC
c, xét tam giác ACE có : AH _|_ AE
AH = HE
=> tam giác ACE cân tại C
d, xét tam giác BMD và tam giác CMA có L BM = MC
AM = MD
^BMD = ^CMA
=> tam giác BMD = tam giác CMA (c-g-c)
=> BD = AC
AC = CE do tam giác ACE cân tại C (câu c)
=> BD = CE