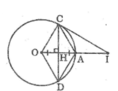
Cho đường tròn(O), bán kính OA, dây CD là trung trực của OA
a) Tứ giác OCAD là hình gì? Vì sao?
b)Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đoạn thẳng OA tại I. Tính CI, biết OA=R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Đồng thời CD ⊥ OA nên ACOD là hình thoi.
b) Vì ACOD là hình thoi nên AC = OC
Mà OC = OA ( = R) nên tam giác OAC đều
Suy ra: ^COA=60∘COA^=60∘ hay ˆCOI=60∘
Mà CI ⊥ OC (tính chất tiếp tuyến)
Trong tam giác vuông OCI, ta có:
CI=OC.tgˆCOI=R.tg60∘=R√3CI=OC.tgCOI^=R.tg60∘=R3.

Vì ACOD là hình thoi nên AC = OC
Mà OC = OA (= R) nên tam giác OAC đều


a/
Ta có
HA=HO (gt)
\(OA\perp CD\left(gt\right)\) => HC=HD (Trong đường tròn đường kính vuông góc với dây cung thì chia đôi dây cung)
=> OCAD là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành)
Mà \(OA\perp CD\left(gt\right)\)
=> OCAD là hình thoi (Hình bình hành có 2 đường chéo vuôn góc là hình thoi)
b/ Kéo dài AO cắt (O) tại K ta có
\(\widehat{ACK}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông ACK có
\(OA=OK\Rightarrow OC=OA=OK=\dfrac{AK}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Mà \(OC=AC\) (cạn hình thoi)
\(\Rightarrow OC=AC=OA\) => tg ACO là tg đều \(\Rightarrow\widehat{AOC}=60^o\)
Mà \(\widehat{AOD}=\widehat{AOC}=60^o\) (trong hình thoi mỗi đường chéo là phân giác của 2 góc đối)
\(\Rightarrow\widehat{AOC}+\widehat{AOD}=\widehat{COD}=60^o+60^o=120^o\)
c/
Xét tg vuông COI có
\(\widehat{CIO}=90^o-\widehat{AOC}=90^o-60^o=30^o\)
\(\Rightarrow OC=\dfrac{1}{2}OI\) (trong tg vuông cạnh đối diện với góc \(30^o\) bằng nửa cạnh huyền
\(\Rightarrow OI=2.OC=2R\)
\(\Rightarrow CI=\sqrt{OI^2-OC^2}\) (Pitago)
\(\Rightarrow CI=\sqrt{4R^2-R^2}=R\sqrt{3}\)
d/
Xét tg COI và tg DOI có
OC=OD=R
OI chung
\(\widehat{AOC}=\widehat{AOD}\) (cmt)
=> tg ACO = tg ADO (c.g.c)\(\Rightarrow\widehat{ODI}=\widehat{OCI}=90^o\) => DI là tiếp tuyến với (O)
e/
Ta có
\(sđ\widehat{COD}=sđcungCD=120^o\) (góc có đỉnh là tâm đường tròn)
\(sđ\widehat{ACD}=\dfrac{1}{2}sđcungCD=60^o\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{ADC}=\dfrac{1}{2}sđcungCD=60^o\) (góc giữa tiếp tuyến và dây cung)
Xét tg ACD có
\(\widehat{CAD}=180^o-\left(\widehat{ACD}+\widehat{ADC}\right)=180^o-\left(60^o+60^o\right)=60^o\)
\(\Rightarrow\widehat{CAD}=\widehat{ACD}=\widehat{ADC}=60^o\) => tg ACD là tg đều
f/
Ta có
\(\widehat{ECD}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow EC\perp CD\)
\(OA\perp CD\left(gt\right)\Rightarrow OI\perp CD\)
=> EC//OI (cùng vuông góc với CD)

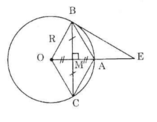
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều = > ∠ A O B = 60 °
Trong tam giác OBE vuông tại B ta có:
B E = O B . t g ∠ A O B = O B . t g 60 ° = R . √ 3

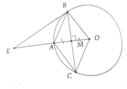
a, OA vuông góc với BC tại M
=> M là trung điểm của BC
=> OCAB là hình thoi
b, Tính được BE = R 3


a) Xét tam giác vuông $MBO$ vuông tại $B$ có đường cao $BH$:
\(\frac{1}{BH^2}=\frac{1}{MB^2}+\frac{1}{BO^2}=\frac{1}{BO^2-HO^2}\)\(\Rightarrow \frac{1}{MB^2}=\frac{1}{27}-\frac{1}{36}=\frac{1}{108}\Rightarrow MB=6\sqrt{3} (\text{cm})\)
b) Thấy rằng $BC$ là trung trực của $AO$ và $AO$ cũng là trung trực của $BC$ nên $BA=BO=OC=AC$
Mặt khác \(\cos(\widehat{BOH})=\frac{1}{2}\) nên \(\cos (\widehat{BOC})\neq 90^0\)
Do đó $OBAC$ là hình thoi
c) Vì $OA$ là trung trực của $BC$ nên với điểm $M\in OA$ thì $MB=MC$ suy ra \(\triangle MBO=\triangle MCO\Rightarrow \widehat {MBO}=\widehat{MCO}=90^0\Rightarrow MC\perp CO\)
Do đó $MC$ là tiếp tuyến của $(O)$