Cho hình thang ABCD (AB song song với CD); O là giao điểm hai đường chéo AC và BD. Đường thẳng qua ô song song với AB cắt AD và BC lần lượt tại M và N.
a. Chứng minh rằng :\(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\)
b. Biết diện tích các tam giác AOB; COD theo thứ tự là a2 ; b2. Hãy tính diện tích hình thang...
Đọc tiếp
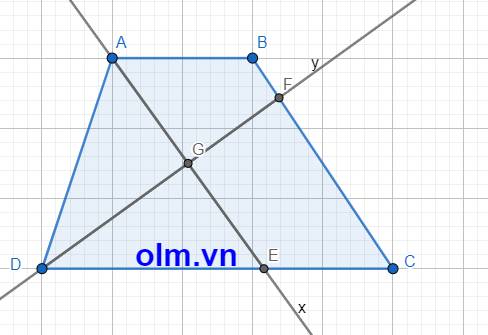
Cho hình thang ABCD (AB song song với CD); O là giao điểm hai đường chéo AC và BD. Đường thẳng qua ô song song với AB cắt AD và BC lần lượt tại M và N.
a. Chứng minh rằng :\(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\)
b. Biết diện tích các tam giác AOB; COD theo thứ tự là a2 ; b2. Hãy tính diện tích hình thang ABCD
còn cần bài này nữa k. mình làm chi tiết cho.
Lời giải:
a) Xem lời giải tại đây:
Câu hỏi của U Suck - Toán lớp 8 | Học trực tuyến
b)
Dễ thấy $\triangle AOB\sim \triangle COD$
$\Rightarrow \frac{S_{AOB}}{S_{COD}}=(\frac{AO}{CO})^2$
$\Leftrightarrow \frac{a^2}{b^2}=(\frac{AO}{CO})^2$
$\Rightarrow \frac{AO}{CO}=\frac{a}{b}$
Do đó:
$\frac{S_{OAB}}{S_{BOC}}=\frac{OA}{OC}=\frac{a}{b}$
$\Rightarrow S_{BOC}=ab$ (m vuông)
$\frac{S_{DOC}}{S_{OAD}}=frac{OC}{OA}=\frac{b}{a}$
$\Rightarrow S_{OAD}=ab$ (m vuông)
Vậy:
$S_{ABCD}=S_{AOB}+S_{BOC}+S_{COD}+S_{DOA}=a^2+ab+b^2+ab=(a+b)^2$ (m vuông)