Cho tam giac ABC đều, M là trung điểm của BC. Trên tia đối của MA lấy E sao cho MA=ME
a,CMR tam gics ABM=ACM
b, Trên tia BC lấy N sao cho Cn=2m. CMR tam giác CAN cân
c, CHo AC=3m. TÍnh AN
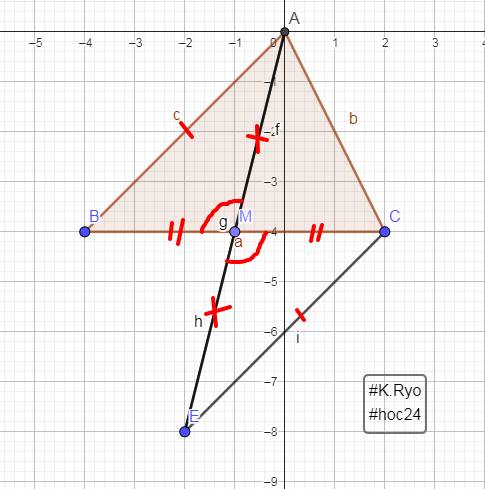
(vẽ hình)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác AMB và tam giác AMC ta có:
AM chung
AB=AC (gt)
MB=MC (vì M là trung điểm của BC)
Suy ra tam giác AMB=tam giác AMC (c-c-c) (đpcm)
b) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc BAM=góc CAM (2 góc tương ứng)
Suy ra AM là tia phân giác của góc BAC (đpcm)
c) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc AMB=góc AMC(2 góc tương ứng)
Mà góc AMB+góc AMC=180 độ (2 góc kề bù)
Suy ra góc AMB=góc AMC=180 độ/2=90 độ
Suy ra AM vuông góc với BC tại M (đpcm)
Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc ACM=góc ABM (2 góc tương ứng) (đpcm)

b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
DO đó: ABEC là hình bình hành
Suy ra: AB//EC

`# \text {DNamNguyenV}`
`a,`
Ta có: M là trung điểm của BC
`=> \text {MB = MC}`
Xét `\Delta ABM` và `\Delta ECM`:
`\text {MA = ME (gt)}`
\(\text{ }\widehat{\text{ AMB}}=\widehat{\text{EMC}}\left(\text{2 góc đối đỉnh}\right)\)
`\text {MB = MC}`
`=> \Delta ABM = \Delta ECM (c - g - c)`
`b,`
Vì `\Delta ABM = \Delta ECM (a)`
`=> \text {AB = CE (2 góc tương ứng)}`

a)xét tam giác ABM và tam giác DCM có:
BN=CM(GT)
góc BMA=góc CMD(đđ)
AM-DM(GT)
\(\Rightarrow\)tam giác ABM=tam giác DCM(c.g.c)
b)theo câu a: tam giác ABM=tam giác DCM
\(\Rightarrow\)góc BAM= góc MDC(2 góc tương ứng)
mà đây là cặp góc so le trong
\(\Rightarrow\)AB//CD
\(\Rightarrow\)góc BAC= góc ACD=90 độ\(\Rightarrow\)CD \(\perp\)AC
c) xét tam giác AHC và tam giác EHC có:
AH=EH(GT)
góc AHC=góc EHC=90 độ
HC chung
\(\Rightarrow\)tam giác AHC = tam giác EHC(c.g.c)
\(\Rightarrow\)CA=CE(2 cạnh tương ứng)
\(\Rightarrow\)tam giác CAE cân tại C

a: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
b:
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
c: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}\) nhọn
=>\(\widehat{ABM}=180^0-\widehat{ABC}>90^0\)
Xét ΔABM có \(\widehat{ABM}>90^0\)
mà AM là cạnh đối diện của góc ABM
nên AM là cạnh lớn nhất trong ΔABM
=>AM>AB
mà AB=AC
nên AM>AC

a) Xét ΔMAB và ΔMEC có
MA=ME(gt)
ˆAMB=ˆEMCAMB^=EMC^(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔMAB=ΔMEC(c-g-c)

Lời giải:
a. Xét tam giác $ABM$ và $ECM$ có:
$BM=CM$ (do $M$ là trung điểm $BC$)
$AM=EM$ (gt)
$\widehat{AMB}+\widehat{EMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle ECM$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{ABM}=\widehat{ECM}$
Mà hai góc này so le trong nên $AB\parallel CE$
c.
$AB\perp AC; AB\parallel CE$
$\Rightarrow AC\perp CE$ (đpcm)
a: Xét ΔABM và ΔECM có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABEC là hình chữ nhật
Suy ra: AB//EC
c: Ta có: ABEC là hình chữ nhật
nên EC\(\perp\)AC
a, Xét \(\Delta ABM\) và \(\Delta CME\) có:
MA=ME(giả thiết)
\(\widehat{M_1}\) =\(\widehat{M_2}\)(đối đỉnh)
MB=MC(M là trung điểm của BC)
\(\Rightarrow\Delta ABM=\Delta ECM\left(c.g.c\right)\)