Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét \(\Delta ABM\) và \(\Delta CME\) có:
MA=ME(giả thiết)
\(\widehat{M_1}\) =\(\widehat{M_2}\)(đối đỉnh)
MB=MC(M là trung điểm của BC)
\(\Rightarrow\Delta ABM=\Delta ECM\left(c.g.c\right)\)

`# \text {DNamNguyenV}`
`a,`
Ta có: M là trung điểm của BC
`=> \text {MB = MC}`
Xét `\Delta ABM` và `\Delta ECM`:
`\text {MA = ME (gt)}`
\(\text{ }\widehat{\text{ AMB}}=\widehat{\text{EMC}}\left(\text{2 góc đối đỉnh}\right)\)
`\text {MB = MC}`
`=> \Delta ABM = \Delta ECM (c - g - c)`
`b,`
Vì `\Delta ABM = \Delta ECM (a)`
`=> \text {AB = CE (2 góc tương ứng)}`
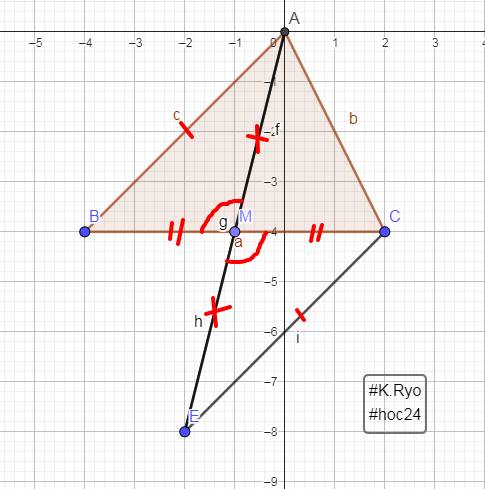

b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
DO đó: ABEC là hình bình hành
Suy ra: AB//EC

Lời giải:
a. Xét tam giác $ABM$ và $ECM$ có:
$BM=CM$ (do $M$ là trung điểm $BC$)
$AM=EM$ (gt)
$\widehat{AMB}+\widehat{EMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle ECM$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{ABM}=\widehat{ECM}$
Mà hai góc này so le trong nên $AB\parallel CE$
c.
$AB\perp AC; AB\parallel CE$
$\Rightarrow AC\perp CE$ (đpcm)
a: Xét ΔABM và ΔECM có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABEC là hình chữ nhật
Suy ra: AB//EC
c: Ta có: ABEC là hình chữ nhật
nên EC\(\perp\)AC

a) Xét tam giác AMB và tam giác AMC ta có:
AM chung
AB=AC (gt)
MB=MC (vì M là trung điểm của BC)
Suy ra tam giác AMB=tam giác AMC (c-c-c) (đpcm)
b) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc BAM=góc CAM (2 góc tương ứng)
Suy ra AM là tia phân giác của góc BAC (đpcm)
c) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc AMB=góc AMC(2 góc tương ứng)
Mà góc AMB+góc AMC=180 độ (2 góc kề bù)
Suy ra góc AMB=góc AMC=180 độ/2=90 độ
Suy ra AM vuông góc với BC tại M (đpcm)
Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc ACM=góc ABM (2 góc tương ứng) (đpcm)

a: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
b:
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
c: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}\) nhọn
=>\(\widehat{ABM}=180^0-\widehat{ABC}>90^0\)
Xét ΔABM có \(\widehat{ABM}>90^0\)
mà AM là cạnh đối diện của góc ABM
nên AM là cạnh lớn nhất trong ΔABM
=>AM>AB
mà AB=AC
nên AM>AC
chịu tau k muốn trả lời