cho A={ x thuộc R / x2-2x<0}
B={ x thuộc R /\(\dfrac{4}{\left|x-3\right|}\)<5
tìm A\B ; B\A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
\(\left(A\cup B\right)\cap C=A\cap C=[1;+\infty)\cap\left(0;4\right)=[1;4)\)
Tập này có 3 phần tử nguyên

Lời giải:
a.
$A=(x+6)^2-(x+2)^2+2[(x-5)^2-(x-3)^2]$
$=(x+6-x-2)(x+6+x+2)+2[(x-5-x+3)(x-5+x-3)]$
$=4(2x+8)+2(-2)(2x-8)$
$=4(2x+8)-4(2x-8)=4[(2x+8)-(2x-8)]=4.16=64$ không phụ thuộc vào $x$
b.
$B=(x^3-2^3)-(x^3+2^3)=-16$ không phụ thuộc vào $x$
c.
$C=x^4+2x^2-[(x^2+3)^2-(2x)^2]$
$=x^4+2x^2-(x^4+6x^2-4x^2)$
$=x^4+2x^2-(x^4+2x^2)=0$ không phụ thuộc vào $x$
a) Ta có: \(A=\left(x+6\right)^2+2\left(x-5\right)^2-\left(x+2\right)^2-2\left(x-3\right)^2\)
\(=x^2+12x+36+2\left(x^2-10x+25\right)-\left(x^2+4x+4\right)-2\left(x^2-6x+9\right)\)
\(=x^2+12x+36+2x^2-20x+50-x^2-4x-4-2x^2+12x-18\)
\(=34\)
b) Ta có: \(B=\left(x-2\right)\left(x^2+2x+4\right)-\left(x+2\right)\left(x^2-2x+4\right)\)
\(=x^3-8-x^3-8\)
=-16
c) Ta có: \(C=x^4+2x^2-\left(x^2-2x+3\right)\left(x^2+2x+3\right)\)
\(=x^4+2x^2-\left[\left(x^2+3\right)^2-4x^2\right]\)
\(=x^4+2x^2-\left(x^4+6x^2+9\right)+4x^2\)
\(=-9\)


Hàm số liên tục trên R trước hết hàm số liên tục tại x=1
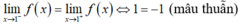
- Vậy không tồn tại a để hàm số liên tục trên R.
\(x^2-2x< 0\)
=>x(x-2)<0
=>0<x<2
\(\dfrac{4}{\left|x-3\right|}< 5\)
\(\Leftrightarrow4-5\left|x-3\right|< 0\)
\(\Leftrightarrow5\left|x-3\right|>4\)
=>x-3>4/5 hoặc x-3<-4/5
=>x>19/5 hoặc x<11/5
A=(0;2)
\(B=\left(-\infty;\dfrac{11}{5}\right)\cup\left(\dfrac{19}{5};+\infty\right)\)
A\B=\(\varnothing\)
B\A=(-\(\infty\);0]\(\cup\left(\dfrac{19}{5};+\infty\right)\)