Một xe chuyển động nhanh dần đều đi trên 2 đoạn đường liên tiếp bằng nhau bằng S0 lần lượt hết 5s và 3,5s. Tính gia tốc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
17 tháng 7 2021
Bạn tham khảo: https://hoc24.vn/cau-hoi/mot-xe-chuyen-dong-nhanh-dan-deu-di-tren-2-doan-duong-lien-tiep-bang-nhau-100m-lan-luot-trong-5s-va-trong-35s-tinh-gia-toc-cua-xe.164124867230
VT
21 tháng 9 2017
Trong một 100m tiếp theo chuyển động hết 3s tức là 200m xe chuyển động hết 8s :
VT
24 tháng 6 2019
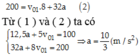
Giải:
Áp dụng công thức s = v 0 t + 1 2 a t 2
Trong 100m đầu tiện : 100 = v 01 .5 + 12 , 5 a 1
Trong một 100m tiếp theo chuyển động hết 3s tức là 200m xe chuyển động hết 8s : 200 = v 01 .8 + 32 a 2
Từ ( 1 ) và ( 2 ) ta có 12 , 5 a + 5 v 01 = 100 32 a + 8 v 01 = 200 ⇒ a = 10 3 ( m / s 2 )
7 tháng 9 2017
gọi v0 là vận tốc ban đầu, a là gia tốc
100m đầu tiên : s1=v0.t1+\(\dfrac{1}{2}\)at12=5v0+12,5a=100 (1)
Cả hai quãng đường : s2=v0.(t1+t2)+\(\dfrac{1}{2}\)a(t1+t2)2=8,5v0+36,125a=200 (2)
giải hê phương trình (1) và (2) ta được v0=14,958(m/s) a=2,017(m/s2)
H9
HT.Phong (9A5)
CTVHS
16 tháng 9 2023
Ta có:
\(s=v_0t+\dfrac{1}{2}at^2\)
100m đầu: \(5v_0+\dfrac{1}{2}\cdot5^2\cdot a=5v_0+12,5a=100\) (1)
200m sau chuyển động trong 8s: \(8v_0+\dfrac{1}{2}\cdot8^2\cdot a=8v_0+32a=200\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}5v_0+12,5a=100\\8v_0+32a=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_0=\dfrac{35}{3}\left(m/s\right)\\a=\dfrac{10}{3}\left(m/s^2\right)\end{matrix}\right.\)
Vậy: ...
18 tháng 11 2021
Trên đoạn đường 100m đi với thời gian 10s:
\(S_1=v_0t+\dfrac{1}{2}at^2=10v_0+\dfrac{1}{2}\cdot a\cdot10^2=100\left(1\right)\)
Trên đoạn đường 200m đi với thời gian 15s:
\(S_2=v_0t+\dfrac{1}{2}at^2=15v_0+\dfrac{1}{2}\cdot a\cdot15^2=200\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow v_0=\dfrac{10}{3}\)m/s và \(a=\dfrac{4}{3}\)m/s2
1,gọi gia tốc là: a
=>he: S1= Vt +0,5at^2=100
S2= (V+at)t +0,5at^2=100
<=> he: S1=5V +25A/2=100
S2=7V/2 +99a/4= 100
<=> V=245/16(m/s)
a=15/8 (m/s^2)
4,tau di: S=5t +0,15t^2
oto: S= 0,25t^2
Gap nhau: 5t +0,15t^2= 0,25t^2
<=> t=50s