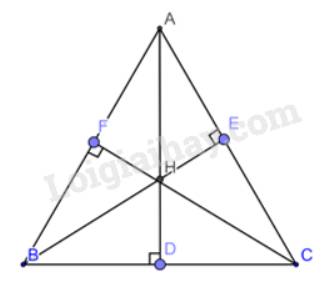
Cho tam giác nhọn ABC, 3 đường cao AD;BE;CF gặp nhau tại H qua 3 đỉnh A,F. Kẻ 3 đường thẳng // BC ; AC, chúng cắt nhau tại M,N. CMR H cách đều 3 đỉnh của Tam giác .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 4 2017
Lại còn phải cm định lý à, xem lại lớp 7. Trong tam giác, 3 đường cao của tam giác cùng đi qua 1 điểm
17 tháng 5 2021
a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AE\cdot AC=AF\cdot AB\)(ĐPCM)
17 tháng 5 2021
b)
Ta có: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(cmt)
nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)
15 tháng 8 2023
a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc DCA chung
=>ΔCDA đồng dạng với ΔCEB
=>CD/CE=CA/CB
=>CD*CB=CA*CE và CD/CA=CE/CB
b; Xét ΔCDE và ΔCAB có
CD/CA=CE/CB
góc C chung
=>ΔCDE đồng dạng với ΔCAB
c:
Xét ΔCAB có
AD,BE là đường cao
AD cắt BE tại H
=>H là trực tâm
=>CH vuông góc AB tại F
góc CEB=góc CFB=90 độ
=>CEFB nội tiếp
=>góc CEF+góc CBF=180 độ
mà góc CEF+góc AEF=180 độ
nên góc AEF=góc CBA
=>góc AEF=góc CED
16 tháng 4 2023
a: Xét ΔAEBvuông tại E và ΔAFC vuông tại F co
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
b: ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
NY
0
1 tháng 4 2023
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiêp
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét ΔDAB vuông tại D và ΔDCH vuông tại D có
góc DAB=góc DCH
=>ΔDAB đồng dạng vơi ΔDCH
=>DA/DC=DB/DH
=>DA*DH=DB*DC
c: Xét ΔHDC vuông tại D và ΔHFA vuông tại F có
góc DHC=góc FHA
=>ΔHDC đồng dạng vơi ΔHFA
=>HD/HF=HC/HA
=>HF*HC=HD*HA
Xet ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE=HD*HA
NH
1
27 tháng 2 2023
Xét ΔAFC vuông tại F và ΔAEB vuông tại E có
CF=BE
góc ACF=gócABE
=>ΔAFC=ΔAEB
=>AC=AB
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
EB=DA
góc C chung
=>ΔCEB=ΔCDA
=>CB=CA=AB
=>ΔABC đều
21 tháng 9 2023
Tham khảo:
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau