 giải chi tiết hộ mk ah
giải chi tiết hộ mk ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(A=\dfrac{1}{\sqrt[3]{a+7b}}+\dfrac{1}{\sqrt[3]{b+7c}}+\dfrac{1}{\sqrt[3]{c+7a}}\)
\(A=\dfrac{\sqrt[3]{64}}{\sqrt[3]{8.8\left(a+7b\right)}}+\dfrac{\sqrt[3]{64}}{\sqrt[3]{8.8\left(b+7c\right)}}+\dfrac{\sqrt[3]{64}}{\sqrt[3]{8.8\left(c+7a\right)}}\)
\(\ge\dfrac{4}{\dfrac{8+8+a+7b}{3}}+\dfrac{4}{\dfrac{8+8+b+7c}{3}}+\dfrac{4}{\dfrac{8+8+c+7a}{3}}\ge\dfrac{\left(2+2+2\right)^2}{\dfrac{8+8+a+7b+8+8+b+7c+8+8+c+7a}{3}}\)
\(=\dfrac{36.3}{8\left(a+b+c\right)+48}=\dfrac{3}{2}\)
Vậy \(A_{min}=\dfrac{3}{2}\Leftrightarrow a=b=c=1\)

Đường thẳng \(\Delta:\left\{{}\begin{matrix}x=1+4t\\y=2-3t\end{matrix}\right.\) đi qua điểm \(A\left(1;2\right)\) và có VTCP \(\overrightarrow{u}=\left(4;-3\right)\)
\(\Rightarrow\overrightarrow{n}=\left(3;4\right)\) là VTPT của đường thẳng
\(\Rightarrow\) PT tổng quát: \(3\left(x-1\right)+4\left(y-2\right)=0\Leftrightarrow3x+4y-11=0\)
\(\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|3.1+4.\left(-1\right)-11\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)

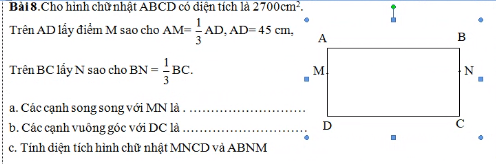
A) Các cạnh song song với MN là : AB,DC
B) Các cạnh vuông góc với DC là AD,DC;BC,CD;MD,DC;NC,CD.
C) Bài giải:
a.Độ dài cạnh AB là :
2700 : 45 = 60 (cm)
Độ dài cạnh AM là :
45 : 3 = 15 ( cm)
Diện tích của hình chữ nhật ABNB là :
60 x 15 = 900 (cm2)
Đ/s : 900 cm2.
b. Độ dài cạnh MD là :
45 - 15 = 30 ( cm)
Do cạnh AB bằng cạnh DC nên diện tích của hình chữ nhật MNCD là :
30 x 60 = 1800 ( cm2)
Đ/s : 1800 cm2
Chúc bn hok tốt.

B11:
theo đề bài, ta có: AB=CD=4cm
BC=AD=3cm
áp dụng ĐL pytago vào tam giác vuông ADB, ta có:
\(AB^2+AD^2=DB^2\Rightarrow BD=5cm\)
ta có công thức: \(AH=\dfrac{AD.AB}{BD}=\dfrac{12}{5}=2,4cm\)
áp dụng ĐL pytago vào tam giác vuông ADH, ta có:
\(AH^2+DH^2=AD^2\\ \Rightarrow DH=1,8cm\)

Lời giải:
a) Nửa chu vi của sân vận động đó hay tổng chiều dài và chiều rộng của sân vận động hình chữ nhật là:
400 : 2 = 200 (m)
Do chiều dài bằng 3232 chiều rộng. Nên coi chiều rộng sân vận động là 2 phần thì chiều dài sân vận động là 3 phần bằng nhau như thế. Ta có sơ đồ như hình vẽ:
Chiều dài: |-----|-----|-----|
Chiều rộng: |-----|-----|
Chiều rộng của sân vận động đó là:
200:(2+3)x2=80 (m)
Chiều dài của sân vận động đó là:
200-80=120 (m)
b) Diện tích của sân vận động đó là:
120x80=9600 (m²)
Đáp án: a) 120m, 80m
b) 9600m²



a) Thay m=3 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}x+3y=3\\3x+4y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+9y=9\\3x+4y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=3\\x+3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{3}{5}\\x=3-3y=3-3\cdot\dfrac{3}{5}=\dfrac{6}{5}\end{matrix}\right.\)
Vậy: Khi m=3 thì hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(\dfrac{6}{5};\dfrac{3}{5}\right)\)

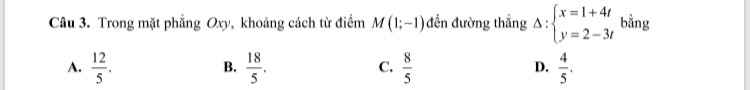

 giải hộ mk ( vẽ hình + chi tiết ah)!!
giải hộ mk ( vẽ hình + chi tiết ah)!! giải chi tiết giúp mk ah
giải chi tiết giúp mk ah



Câu 4:
\(\dfrac{3x+5}{16}-\dfrac{3x-5}{26}=\dfrac{3x-8}{29}-\dfrac{3x+8}{13}\)
\(\Leftrightarrow\left(\dfrac{3x+5}{16}+1\right)-\left(\dfrac{3x-5}{26}+1\right)=\left(\dfrac{3x-8}{29}+1\right)-\left(\dfrac{3x-8}{13}+1\right)\)
\(\Leftrightarrow\left(3x+21\right)\left(\dfrac{1}{16}-\dfrac{1}{26}-\dfrac{1}{29}+\dfrac{1}{13}\right)=0\)
=>3x+21=0
hay x=-7