Question

[Sách Giáo Khoa]

Rada của một máy bay trực thăng theo dõi chuyển động của một oto trong 10 phút, phát hiện rằng vẫn tốc v của oto thay đổi phụ thuộc vào thời gian bởi công thức : \(x=3t^2-30t+135,\)

(t tính bằng phút, v tính bằng km/h).

a) Tính vận tốc của oto khi t = 5 phút.

b) Tính giá trị của t khi vận tốc oto bằng 120km/h (làm tròn kết quả tới chữ số thập phân thứ hai).

Answer 1

[Quốc Đạt]

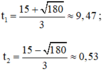
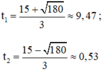
a) Khi t = 5 (phút) thì v = 3 . 5² – 30 . 5 + 135 = 60 (km/h)

b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t² – 30t + 135

Hay t² – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.

∆’ = 5² – 5 = 25 – 5 = 20, √∆’ = 2√5

t₁ = 5 + 2√5 ≈ 9,47, t₂ = 5 - 2√5 ≈ 0,53

Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t₁ ≈ 9,47 (phút), t₂ ≈ 0,53 (phút).

Answer 2

[Đặng Phương Nam]

a) Khi t = 5 (phút) thì v = 3 . 5² – 30 . 5 + 135 = 60 (km/h)

b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t² – 30t + 135

Hay t² – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.

∆’ = 5² – 5 = 25 – 5 = 20, √∆’ = 2√5

t₁ = 5 + 2√5 ≈ 9,47, t₂ = 5 - 2√5 ≈ 0,53

Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t₁ ≈ 9,47 (phút), t₂ ≈ 0,53 (phút).