Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi v = 120 km/h
⇔ 3t2 – 30t + 135 = 120
⇔ 3t2 – 30t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ’ = b’2 – ac = (-15)2 – 3.15 = 180
Phương trình có hai nghiệm phân biệt
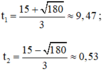
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t1 và t2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

a) Tại t = 5, ta có: v = 3 . 5 2 – 30 . 5 + 135 = 60 ( k m / h )
b) Khi v = 120 km/h
⇔ 3 t 2 – 30 t + 135 = 120 ⇔ 3 t 2 – 30 t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ ’ = b ’ 2 – a c = ( - 15 ) 2 – 3 . 15 = 180
Phương trình có hai nghiệm phân biệt
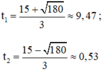
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t 1 v à t 2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

mọi người ơi giúp mình với ![]() nagyf mai là hạn chót nộp bài r
nagyf mai là hạn chót nộp bài r

Gọi x và y lần lượt là vận tốc của xe ô tô A và xe ô tô B .
Sau 2h hai xe gặp nhau nên ta có phương trình :
\(2x+2y=150\Rightarrow x+y=75\) (1)
Vận tốc xe ô tô A tăng thêm 5km/h và vận tốc của ô tô B giảm 5km/h thì vận tốc ô tô A bằng 2 lần vận tốc ô tô B nên ta có :
\(x+5=2\left(y-5\right)\Leftrightarrow x-2y=-15\)(2)
Từ (1) và (2) ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=75\\x-2y=-15\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=45\\y=30\end{matrix}\right.\)

gọi vận tốc oto đi từ a là x
vận tốc đi từ b là y (0<x,y<150)
do sau 2 h 2 oto gặp nhau nên ta có pt
2x+2y=150 (1)
do vận tốc đi từ a tăng 15km/h thì bằng 2 lần vận tốc đi từ b nên ta có pt
x-2y=-15 (2)
từ 1 và 2 ta có hệ pt
\(\left\{{}\begin{matrix}2x+2y=150\\x-2y=-15\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=45\\y=30\end{matrix}\right.\)tmđk
vậy vận tốc 2 xe là 45km/h và 30km/h
a) Khi t = 5 (phút) thì v = 3 . 52 – 30 . 5 + 135 = 60 (km/h)
b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t2 – 30t + 135
Hay t2 – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.
∆’ = 52 – 5 = 25 – 5 = 20, √∆’ = 2√5
t1 = 5 + 2√5 ≈ 9,47, t2 = 5 - 2√5 ≈ 0,53
Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t1 ≈ 9,47 (phút), t2 ≈ 0,53 (phút).
a) Khi t = 5 (phút) thì v = 3 . 52 – 30 . 5 + 135 = 60 (km/h)
b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t2 – 30t + 135
Hay t2 – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.
∆’ = 52 – 5 = 25 – 5 = 20, √∆’ = 2√5
t1 = 5 + 2√5 ≈ 9,47, t2 = 5 - 2√5 ≈ 0,53
Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t1 ≈ 9,47 (phút), t2 ≈ 0,53 (phút).