Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tại t = 5, ta có: v = 3 . 5 2 – 30 . 5 + 135 = 60 ( k m / h )
b) Khi v = 120 km/h
⇔ 3 t 2 – 30 t + 135 = 120 ⇔ 3 t 2 – 30 t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ ’ = b ’ 2 – a c = ( - 15 ) 2 – 3 . 15 = 180
Phương trình có hai nghiệm phân biệt
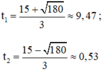
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t 1 v à t 2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

Khi v = 120 km/h
⇔ 3t2 – 30t + 135 = 120
⇔ 3t2 – 30t + 15 = 0
Có a = 3; b’ = -15; c = 15; Δ’ = b’2 – ac = (-15)2 – 3.15 = 180
Phương trình có hai nghiệm phân biệt
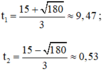
Vì rada quan sát chuyển động của ô tô trong 10 phút nên t1 và t2 đều thỏa mãn.
Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

a) Khi t = 5 (phút) thì v = 3 . 52 – 30 . 5 + 135 = 60 (km/h)
b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t2 – 30t + 135
Hay t2 – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.
∆’ = 52 – 5 = 25 – 5 = 20, √∆’ = 2√5
t1 = 5 + 2√5 ≈ 9,47, t2 = 5 - 2√5 ≈ 0,53
Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t1 ≈ 9,47 (phút), t2 ≈ 0,53 (phút).
a) Khi t = 5 (phút) thì v = 3 . 52 – 30 . 5 + 135 = 60 (km/h)
b) Khi v = 120 (km/h), để tìm t ta giải phương trình 120 = 3t2 – 30t + 135
Hay t2 – 10t + 5 = 0. Có a = 1, b = -10, b’ = -5, c = 5.
∆’ = 52 – 5 = 25 – 5 = 20, √∆’ = 2√5
t1 = 5 + 2√5 ≈ 9,47, t2 = 5 - 2√5 ≈ 0,53
Vì rađa chỉ theo dõi trong 10 phút nên 0 < t < 10 nên cả hai giá trị của t đều thích hợp. Vậy t1 ≈ 9,47 (phút), t2 ≈ 0,53 (phút).

Gọi x ( km/h ) là vận tốc dự dịnh của ô tô và y ( giờ ) là thời gian dự định đi của ô tô . ĐK : ( x , y > 0 )
Nếu vận tốc ô tô giảm 10 km/h thì thời gian tăng 45 phút nên ta có phương trình : ( x - 10 )( y + \(\dfrac{3}{4}\)) = xy ⇔ xy + x\(\dfrac{3}{4}\) - 10y - \(\dfrac{15}{2}\) = xy
⇔ \(x\dfrac{3}{4} - 10y = \dfrac{15}{2}\) (1)
Nếu vận tốc của ô tô tăng 10 km/h thì thời gian giảm 30 phút nên ta có phương trình : ( x + 10 )( y - \(\dfrac{1}{2}\) ) = xy ⇔ - \(\dfrac{-1}{2}x\) + 10y = 5 (2)
Từ (1) và (2) ta có hpt giải ra dc x vs y

30 phút = 1/2 giờ;
45 phút = 3/4 giờ
Gọi vận tốc dự định của ô tô là x (km/h) và thời gian dự định đi của ô tô là y (giờ)
Điều kiện : x > 10; y > 1/2
Lúc đó quãng đường đi của ô tô từ A đến B là x.y (km/h)
Vì ô tô tăng vận tốc lên 10 km/h thì đến B trước 30 phút nên ta có phương trình:
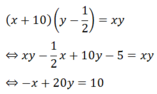
Vận tốc ô tô giảm đi 10 km/h thì đến B chậm hơn 45 phút nên ta có phương trình:
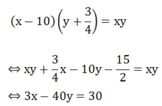
Ta có hệ phương trình
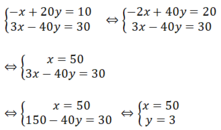
Vậy vận tốc dự định đi của ô tô là 50km/h và thời gian dự định đi của ô tô là 3 giờ.

goi a la van toc ban dau, b la thoi gian ban dau,s la quang duong
ta co:a.b=s,(a-10)(b+0,75)=s,(a+10)(b-0,5)=s
$\Rightarrow$⇒ab+a.0,75-10b-7,5=s va ab-0,5a+10b-5=s
do ab =s nen a.0,75-10b-7,5=0 va -0,5a+10b-5=0
cong 2 ve tren $\Rightarrow$⇒0,25.a=12,5 nen a=50 va t=3
Đúng 1000000..0 Không đúng 0
mọi người ơi giúp mình với nagyf mai là hạn chót nộp bài r
nagyf mai là hạn chót nộp bài r