cho tam giác ABC với M,N lần lượt là trung điểm của hai cạnh AB,AC. xác định độ dài của vec tơ AB và AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 6 2019
a) Đo độ dài rồi viết tiếp vào chỗ chấm:
- Độ dài cạnh AB là 4cm.
- Độ dài cạnh AC là 6cm.
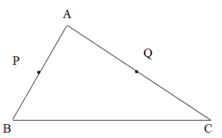
b) Xác định trung điểm P của canh AB và trung điểm Q của cạnh AC.
XO
21 tháng 8 2018
Nối BN.
*Xét tam giác AMN và tam giác ABN có :
- Đáy AM = 1/2 đáy AB
- Chung chiều cao hạ từ đỉnh N
=> S tam giác AMN = 1/2 S tam giác ABN
S tam giác ABN là 4 : 1/2 = 8 (cm2)
* Xét tam giác ABN và tam giác ABC có:
- Đáy AN = 1/2 Đáy AC
- Chung chiều cao hạ từ đỉnh B
=> S tam giác ABN = 1/2 S tam giác ABC
S tam giác ABC là : 8 : 1/2 = 16 (cm2)
Đáp số 16 cm2
8 tháng 12 2021
a: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{A}\) chung
AN=AM
Do đó: ΔABN=ΔACM
Suy ra: BN=CM
2 tháng 12 2015
1) Gọi cạnh tam giác đều là a => đường cao h =\(\frac{a\sqrt{3}}{2}\)=
mà h = 3/2R => \(\frac{a\sqrt{3}}{2}\)=\(\frac{3}{2}.\frac{4}{3}\) =2=> a =\(\frac{4}{\sqrt{3}}\)
S =ah/2 =\(\frac{4}{\sqrt{3}}\).2/2 =\(\frac{4}{\sqrt{3}}\)
2) ABC vuông tại A ( 62+82 =102)
M là điểm chính giữa => AM =CM => OM là trung trực AC => Tam giác OIC vuông tại I
=> OI = \(\sqrt{OC^2-IC^2}=\sqrt{5^2-4^2}=3\)
2 tháng 12 2015
câu 2 ; theo đề bài ta có tam giác ABC vuông tại A
VÌ OM là đường kính đi qua dây AC nên OM vuông góc với AC hay OI vuông góc với AC và AI=IC[tính chất đường kính]
Do đó OI song song với AB[cùng vuông góc với AC]
theo định lí ta-lét ta có \(\frac{OI}{AB}=\frac{IC}{AC}\)
mà IC=AC =8/2=4 cm
thay vào giải ra OI=6*4/8=3 cm
còn câu 1 tớ cũng đang định hỏi đây
Mình vẫn chưa thấy vai trò của $M,N$ trong bài toán này. Bạn xem lại đề.