| tam giác | dinh | cạnh bên |
| tam giác AMEcan tai A | A | AM=AE=2cm |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
1
Những câu hỏi liên quan
26 tháng 1 2016
Dễ mà p áp dụng Pytago câu a, còn mấy câu kia mìh lm` biến vẽ hìh Cm qá p ơi.
30 tháng 1 2021
a) Xét ΔAME vuông tại E và ΔAMF vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)(AM là tia phân giác của \(\widehat{FAE}\))
Do đó: ΔAME=ΔAMF(cạnh huyền-góc nhọn)
Ta có: AM là tia phân giác của \(\widehat{BAC}\)(cmt)
nên \(\widehat{BAM}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{EAM}=45^0\)
Xét ΔEAM vuông tại E có \(\widehat{EAM}=45^0\)(cmt)
nên ΔEAM vuông cân tại E(Dấu hiệu nhận biết tam giác vuông cân)
hay AE=ME(hai cạnh bên)(đpcm)
b) Ta có: AE=ME(cmt)
mà AE=2cm(gt)
nên ME=2cm
Áp dụng định lí Pytago vào ΔEBM vuông tại E, ta được:
\(BM^2=BE^2+ME^2\)
\(\Leftrightarrow BM^2=1^2+2^2=5\)
hay \(BM=\sqrt{5}cm\)
Vậy: \(BM=\sqrt{5}cm\)
CN
2
NM
19 tháng 3 2017
cậu học tính chất 3 đường phân giác chưa.Nếu học rồi thì trả lời tớ nhé
24 tháng 3 2023
A B B C D E H
Xét \(\Delta AEC\&\Delta ADB\\ \) có:
\(\widehat{A}=\widehat{A}\\ \widehat{E}=\widehat{D}=90^o\\ \Rightarrow\Delta AEC\sim\Delta ADB\left(đpcm\right)\)
b) vì\(\Delta AEC\sim\Delta ADB\Leftrightarrow\dfrac{AB}{AE}=\dfrac{AC}{AD}\Leftrightarrow\dfrac{3}{AE}=\dfrac{5}{2}\Rightarrow AE=\dfrac{3\cdot2}{5}=1.2cm\)
KV
24 tháng 3 2023
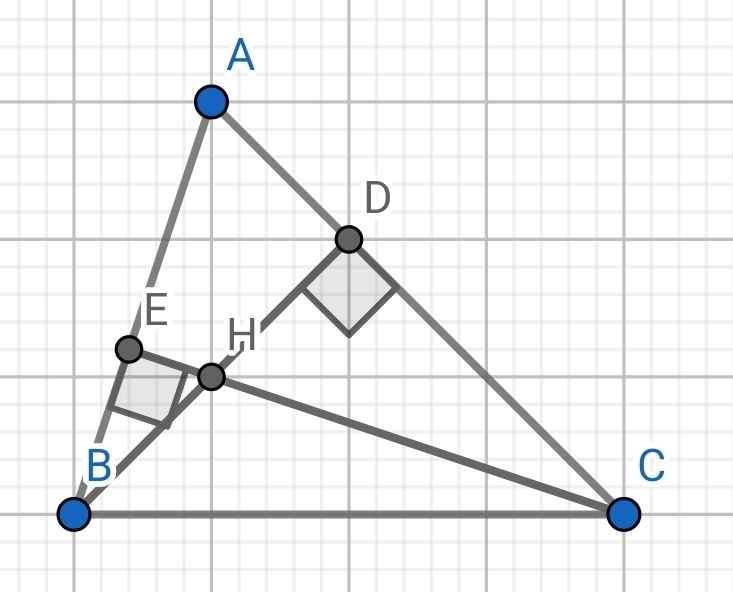
a) Xét ∆ADB và ∆ACE có:
∠ADB = ∠ACE = 90⁰
∠A chung
⇒ ∆ADB ∽ ∆ACE (g-g)
b) Do ∆ADB ∽ ∆ACE (cmt)
⇒ AD/AC = AB/AE
⇒ AE = AB.AC/AD
= 2.3/5
= 1,2 (cm)
4 tháng 3 2017
Bài giải :
Sabi = 2 * Sbie
Sbic = 3 * Sbie
suy ra : Sabi / Sbic = 2/3
Said / Scid = 2/3 suy ra Scid = 16 : 2 * 3
= 24 ( cm2 )
suy ra : Saic = 24 + 16 = 40 ( cm2 )
Saec = 2/3 Saic = 3/2 * 40 = 60 ( cm2 )
Saec = 3/2 * 60 = 90 ( cm2 )
30 tháng 12 2020
cho tam giác abc vuông tại A (AB<AC) ke Ah vuông với bc tại h trê cạnh ac lấy điểm d sao cho ad=ah gọi e là trung điểm của hd tia ae cắt bc tai f cm a) tam giác ahe= tam giác ade và ae vuông tại hd b) tam giác ahf = tam giác adf c) góc dfc= góc abc
Đề bài yêu cầu gì?