E F G m Trong hình bên ta có tam giác EFG và tia FmCMR:góc GEm= góc EFG+ góc...
Đọc tiếp
Trong hình bên ta có tam giác EFG và tia Fm
CMR:góc GEm= góc EFG+ góc EGF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
18 tháng 12 2018
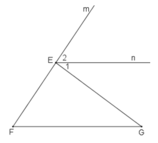
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.
CA
4 tháng 10 2017
EFG
+
EGF
=
GEm
suy ra G+F=m dư 1
m+1=E
mình nói đến đây thôi nha vì mình học lớp 6
28 tháng 10 2017
Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm
20 tháng 7 2021
c) Xét tứ giác FMHN có
\(\widehat{NFM}=90^0\)
\(\widehat{FNH}=90^0\)
\(\widehat{FMH}=90^0\)
Do đó: FMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Hình chữ nhật FMHN có đường chéo FH là tia phân giác của \(\widehat{NFM}\)(gt)
nên FMHN là hình vuông(Dấu hiệu nhận biết hình vuông)
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
14 tháng 12 2022
Xét ΔOAD có OE/OA=OF/OD
nên EF//AD và EF=AD/2=BC/2
Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
DO đó: ΔADC=ΔBCD
=>góc ODC=góc OCD=60 đọ
=>ΔODC đều
mà CF là trung tuyến
nên CF vuông góc với BD
ΔBFC vuông tại F
mà FG là trung tuyến
nên FG=BC/2
Xét ΔOAB có góc OBA=góc OAB và góc AOB=60 độ
nên ΔOAB đều
mà BE là trung tuyến
nên BE vuông góc với CE
ΔBEC vuông tại E
mà EG là trung tuyến
nên EG=BC/2
=>EG=EF=FG
=>ΔEFG đều
WH
3 tháng 5 2018
Trả lời
Xét tam giác OAD ta có: OE=AE; OE=FD \(\Rightarrow\)EF là ĐTB của tam giác OAD
\(\Rightarrow EF=\frac{1}{2}AD=\frac{1}{2}BC\left(1\right)\)và EF//AD
Ta có tam giác ABCD là tâm giác cân \(\Rightarrow\widehat{OCD}\)\(=\widehat{ODC}\)=\(60^0\)(tự lập luận)
Ta có: Tam giác ODC đều có CF là đường trung tuyến đồng thời là đường cao
\(\Rightarrow CF\perp BD\)
Tam giác BFC vuông tại F có FG là đường trung tuyến
\(\Rightarrow FG=CG=BG=\frac{BC}{2}\)(Theo t/c đường trung tuyến trong \(\Delta\)vuông)(2)
Chứng minh tường tự: EG=\(\frac{BC}{2}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow FG=EF=EG\Rightarrow\Delta EFG\)là tam giác đều
Tổng 3 góc ∆ =180°=> góc FEG = 180 - EFG-EGF
Mà FEG và GEm bù nhau => FEG= 180-GEm
=> EFG +EGF = GEm