Chứng minh a+b<ab . Biết a>2 ;b>2 và a;b trong N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2019
Vì a ≥ 0 nên a xác định, b ≥ 0 nên b xác định
Ta có: a - b 2 ≥ 0 ⇒ a - 2 a b + b ≥ 0 ⇒ a + b ≥ 2 a b
⇒ a + b + a + b ≥ a + b + 2 a b
⇒ 2(a + b) ≥ a 2 + 2 a b + b 2
HD
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2021
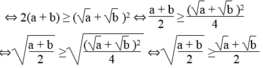
\(\Leftrightarrow\dfrac{a^4+b^4+4a^2b^2}{a^2b^2}\ge\dfrac{3\left(a^2+b^2\right)}{ab}\)
\(\Leftrightarrow a^4+b^4+4a^2b^2\ge3ab\left(a^2+b^2\right)\)
\(\Leftrightarrow\left(a^4+b^4-2a^2b^2\right)+6a^2b^2-3ab\left(a^2+b^2\right)\ge0\)
\(\Leftrightarrow\left(a^2-b^2\right)^2-3ab\left(a^2+b^2-2ab\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a+b\right)^2-3ab\left(a-b\right)^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+b^2-ab\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left[\left(a-\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\right]\ge0\) (luôn đúng)
19 tháng 2 2022
a: \(VT=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: Bạn ghi lại đề đi bạn
18 tháng 2 2022
a: \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+b^2d^2-2abcd+a^2d^2-2abcd+b^2c^2\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: \(\left(ac+bd\right)^2< =\left(a^2+b^2\right)\left(c^2+d^2\right)\)
\(\Leftrightarrow a^2c^2+2abcd+b^2d^2-a^2c^2-a^2d^2-b^2c^2-b^2d^2< =0\)
\(\Leftrightarrow-a^2d^2+2abcd-b^2c^2< =0\)
\(\Leftrightarrow\left(ad-bc\right)^2>=0\)(luôn đúng)
R
18 tháng 2 2022
a) \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+2abcd+b^2d^2+a^2d^2-2adbc+b^2c^2\)
\(=a^2c^2+b^2d^2+a^2d^2+b^2c^2\)
\(=\left(a^2c^2+a^2d^2\right)+\left(b^2d^2+b^2c^2\right)\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
b) \(\left(a^2+b^2\right)\left(c^2+d^2\right)-\left(ac+bd\right)^{^2}\)
\(=a^2c^2+a^2d^2+b^2c^2+b^2d^2-a^2c^2-2abcd-b^2d^2\)
\(=a^2d^2+b^2c^2-2abcd\)
\(=\left(ad\right)^2-2ad.bc+\left(bc\right)^2\)
\(=\left(ad-bc\right)^2\ge0\)
\(=\left(ac+bd\right)^2\le\left(a^2+b^2\right)\left(c^2+d^2\right)\)
PT
1
CM
31 tháng 7 2019
Biến đổi vế trái ta có:
VT = (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 )
= a 3 + b 3 + a 3 – b 3 = 2 a 3 = VP
Vế trái bằng vế phải nên đẳng thức được chứng minh.
NT
4
TA
17 tháng 7 2021
VP `=(a+b)(a^2-ab+b^2)`
`=a^3-a^2b+ab^2+a^2b-ab^2+b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)+b^3`
`=a^3+b^3`
.
VP `=(a-b)(a^2+ab+b^2)`
`=a^3+a^2b+ab^2-a^2b-ab^2-b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)-b^3`
`=a^3-b^3`
11 tháng 2 2022
a) Ta có (ac+bd)2+(ad−bc)2=a2c2+2acbd+b2d2+a2d2−2adbc+b2c2
=(a2c2+b2c2)+(a2d2+b2d2)=c2(a2+b2)+d2(a2+b2)=(a2+b2)(c2+d2)
b) Ta có 0≤(ad−bc)2⇔(ac+bd)2≤(ac+bd)2+(ad−bc)2
Mà theo câu a, ta có (ac+bd)2+(ad−bc)2=(a2+b2)(c2+d2)
Nên (ac+bd)2≤(a2+b2)(c2+d2)
NN
2
DT
Dang Tung
CTVHS
12 tháng 6 2023
Sửa đề : \(\dfrac{a^2}{a^2+b}+\dfrac{b^2}{b^2+a}\le1\\ \) (*)
\(< =>\dfrac{a^2\left(b^2+a\right)+b^2\left(a^2+b\right)}{\left(a^2+b\right)\left(b^2+a\right)}\le1\\ < =>a^2b^2+a^3+b^2a^2+b^3\le\left(a^2+b\right)\left(b^2+a\right)\) ( Nhân cả 2 vế cho `(a^{2}+b)(b^{2}+a)>0` )
\(< =>a^3+b^3+2a^2b^2\le a^2b^2+b^3+a^3+ab\\ < =>a^2b^2\le ab\\ < =>ab\le1\) ( Chia 2 vế cho `ab>0` )
Do a,b >0
Nên áp dụng BDT Cô Si :
\(2\ge a+b\ge2\sqrt{ab}< =>\sqrt{ab}\le1\\ < =>ab\le1\)
Do đó (*) luôn đúng
Vậy ta chứng minh đc bài toán
Dấu "=" xảy ra khi : \(a=b>0,a+b=2< =>a=b=1\)
LD
22 tháng 7 2023
a Sửa đề : Chứng minh \(\dfrac{a^2}{a^2+b}\)+\(\dfrac{b^2}{b^2+a}\)\(\le\) 1 ( Đề thi vào 10 Hà Nội).
Bất đẳng thức trên tương đương :
\(\dfrac{a^2+b-b}{a^2+b}\)+\(\dfrac{b^2+a-a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\) 1 - \(\dfrac{b}{a^2+b}\)+ 1 - \(\dfrac{a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\)1 - \(\dfrac{b}{a^2+b}\) - \(\dfrac{a}{b^2+a}\)\(\le\)0
\(\Leftrightarrow\)- \(\dfrac{b}{a^2+b}\)- \(\dfrac{a}{b^2+a}\)\(\le\)-1
\(\Leftrightarrow\)\(\dfrac{a}{b^2+a}\)+ \(\dfrac{b}{a^2+b}\)\(\ge\)1
Xét VT = \(\dfrac{a^2}{ab^2+a^2}\)+ \(\dfrac{b^2}{a^2b+b^2}\)\(\ge\)\(\dfrac{\left(a+b\right)^2}{ab^2+a^2+a^2b+b^2}\) (Cauchy - Schwarz)
= \(\dfrac{\left(a+b\right)^2}{ab\left(b+a\right)+a^2+b^2}\)
\(\ge\)\(\dfrac{\left(a+b\right)^2}{2ab+a^2+b^2}\)
= \(\dfrac{\left(a+b\right)^2}{\left(a+b\right)^2}\)= 1
Vậy BĐT được chứng minh
Dấu '=' xảy ra \(\Leftrightarrow\)a = b = 1