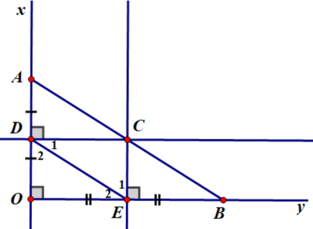
Cho góc vuông xOy , điểm A thuộc tia Ox , B thuộc tia Oy . Đường trung trực của OA cát Ox tại D , đường trung trực của OB cắt Oy ở E . Gọi C là giao điểm của hai đường trung trực đó . Cm
a,CE = OD
b, CE vuông góc CD
c,CA=CB
d,CA//DE
e, A,B,C thẳng hàng

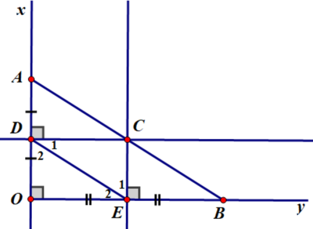

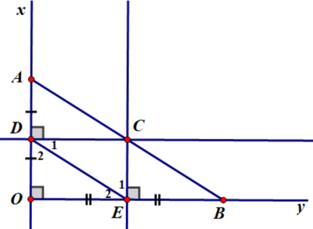

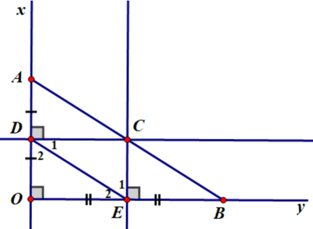

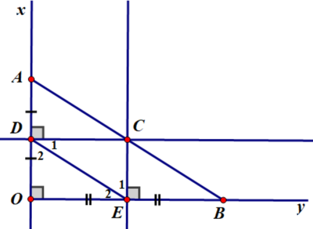

a: Xét tứ giác ODCE có
OD//CE
OE//CD
Do đó: ODCE là hình bình hành
Suy ra: CE=OD
b: Hình bình hành ODCE có \(\widehat{EOD}=90^0\)
nên ODCE là hình chữ nhật
Suy ra: CE\(\perp\)CD
d: Xét tứ giác CEDA có
CE//DA
CE=DA
Do đó: CEDA là hình bình hành
Suy ra: CA//DE