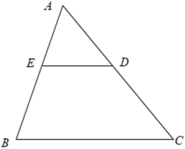
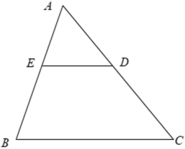
cho Δ ABC có AB=AC,trên hai cạnh AB và AC lần lượt lấy điểm D và E sao cho AD=AE,CMR:a,góc B=C
b,DE//BC.KHÔNG SỬ DỤNG ΔABC LÀ TAM GIÁC CÂN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2016
a)Trên cạnh BC lấy điểm M sao cho BM = CM
Xét tam giác AMB và tam giác AMC có :
AM: chung
BM=CM
AB=AC
=> tam giác AMB= tam giác AMC ( c.c.c)
=> góc B=góc C
b) Gọi giao điểm của DE và AM là K
Theo câu a) tam giác AMB = tam giác AMC
=> góc AMB = góc AMC và góc BAM= góc CAM
Ta có góc AMB = góc AMC
Mà góc AMB và góc AMC là 2 góc kề bù nên góc AMB= góc AMC= 90 độ
=> BC vuông góc với AM
Xét tam giác AKD và tam giác AKE có :
AD=AE ( gt)
góc DAK= góc EAK
AK chung
=> tam giác AKD = tam giác AKE ( c.g.c)
=> góc AKD = góc AKE
Mà góc AKD và góc AKE là 2 góc kề bù nên góc AKD=góc AKE=90 độ
=. DE vuông góc vs AM
Vì DE và BC cung vuông góc vs AM nên DE//BC
3 tháng 8 2016
a) Ta có: AB = AC (gt)
=> Góc B = Góc C ( quan hệ giữa góc và cạnh đối diện)
b) Ta có: AD = AE (gt)
=> Góc ADE = Góc AED ( quan hệ giữa góc và cạnh đối diện) => tam giác ADE cân tại A
Vì 2 tam giác này cùng cân tại A nên:
Ta có: góc B = góc C = \(\frac{180-A}{2}\)
Ta lại có: góc ADE = góc AED (cmt) =\(\frac{180-A}{2}\)
=> Góc ADE = góc ABC
Mà 2 góc này ở vị trí đồng vị => DE//BC
HN
2 tháng 8 2016
a) Xét \(\Delta ABC\) có: \(AB=AC\left(gt\right)\)
\(\Rightarrow\)\(\Delta ABC\) cân tại A (t/c)
\(\Rightarrow\)\(\widehat{B} = \widehat{C} = \frac{180^O - \widehat{A}}{2}\)(t/c)
b) Xét \(\Delta ADE\) có: \(AD=AE\left(gt\right)\)
\(\Rightarrow\)\(\Delta ADE \) cân tại A (t/c)
\(\Rightarrow\)\(\widehat{D} = \widehat{E} = \frac{180^O - \widehat{A}}{2}\)
\(\Rightarrow\)\(\widehat{B} = \widehat{D}\) (Vì cùng bằng \(\frac{180^O - \widehat{A}}{2}\))
mà 2 góc này nằm ở vị trí đồng vị
\(\Rightarrow\)\(BD//CE (dpcm)\)
1 tháng 8 2016
a) Xét ΔABC có AB=AC(gt)
=>ΔABC cân tại A
=>\(\widehat{B}=\widehat{C}\)
b)Vì ΔABC cân tại A(gt)
=>\(\widehat{ABC}=\frac{180-\widehat{A}}{2}\) (1)
Xét ΔADE có: AD=AE(gt)
=>ΔADE cân tại A
=>\(\widehat{ADE}=\frac{180-\widehat{A}}{2}\) (2)
Từ (1) (2) suy ra:
\(\widehat{ABC}=\widehat{ADE}\)
Mà hai góc này ở vị trí đồng vị
=>DE//BC
14 tháng 8 2023
a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
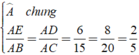
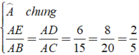
a) nối DC; nối BE
xét tam giác ADC và tam giác AEB có:
AD=AE(gt)
AB=AC(gt)
góc A(chung)
=> tam giác ADC= tam giác AEB(c.g.c)
=> DC=BE
ta có: BD=AB-AD
EC=AC-AE
AB=AC
AE=AD
=> BD=EC
xét tam giác DBC và tam giác ECB có:
BD=EC(cmt)
DC=BE(cmt)
BC(chung)
=> tam giác DBC= tam giác ECB(c.c.c)
=> góc B= góc C
b)
ta có: AD=AE=> tam giác AED cân tại A
=> góc ADE=(180*-A)/2
ta có tam giác ABC có góc B=góc C
=> gócB=(180*-A)/2
=> góc ADE= góc ABC
=> DE//BC