K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

12 tháng 5 2023
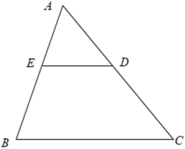
1,3: Xet ΔADE và ΔACB có
AD/AC=AE/AC
góc DAE=góc CAB
=>ΔADE đồng dạng vói ΔACB
=>góc ADE=góc ACB
=>DE//BC
2: DE/CB=AD/AC=3/10

CM
22 tháng 9 2019
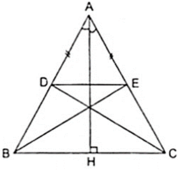
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.

H
2 tháng 5 2017
Xét tam giác AED Và Tam giác ABC có : Góc A chung và \(\frac{AE}{AB}=\frac{6}{15}=\frac{2}{5},\frac{AD}{AC}=\frac{8}{20}=\frac{2}{5}\) suy ra tam giác AED đồng dạng với tam giác ABC (cgc) suy ra \(S_{AED}:S_{ABC}=\left(\frac{AE}{AB}\right)^2=\left(\frac{2}{5}\right)^2=\frac{4}{25}\)
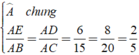
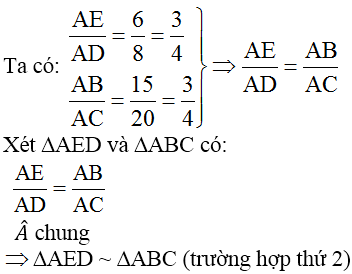
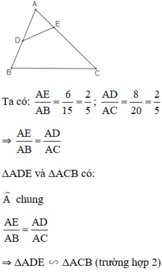
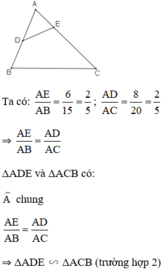
Xét Δ AED và Δ ABC có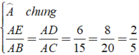
⇒ Δ AED ∼ Δ ABC ( c - g - c )