Giải phương trình: \(sin3x-cos3x+sinx+cosx=\dfrac{1}{sin3x+cosx}-\dfrac{1}{cos3x-sinx}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 7 2022
b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)
c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)
\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)
NT
1
HT
7 tháng 4 2021
Ok sau đây là 3 cách, mà mình thấy c3 chả được xài cách nào :( Cơ mà thoi kệ
Cách 3:
P/s: Hmm, thực ra thì ban đầu mình cũng nghĩ là sử dụng ngắt VCB tương đương k được đâu, bởi nó chỉ sử dụng cho tích và thương, cơ mà nó áp dụng cho tổng và hiệu khi mà 2 hạng tử mình biến đổi ra ko tương đương nhau, vậy nên cách 1 vẫn được chấp nhận nhé. Mình sẽ dele 2 câu trả lời kia để gộp 3 cách làm 1 câu trl cho tiện.
PT
1
CM
26 tháng 2 2018
Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
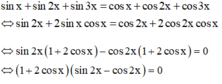
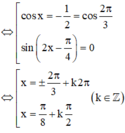
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
\(\Leftrightarrow cos3x+\sqrt{3}sin3x=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow\dfrac{1}{2}cos3x+\dfrac{\sqrt{3}}{2}sin3x=\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{3}\right)=cos\left(x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{3}=x-\dfrac{\pi}{6}+k2\pi\\3x-\dfrac{\pi}{3}=\dfrac{\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
TP
1
TX
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 6 2020
\(\frac{\left(sin3x+cosx\right)sin3x+\left(cos3x+sinx\right)cos3x}{cos4x}\)
\(=\frac{sin^23x+sin3x.cosx+cos^23x+cos3x.sinx}{cos4x}=\frac{1+sin3x.cosx+cos3x.sinx}{cos4x}\)
\(=\frac{1+sin4x}{cos4x}=\frac{sin^22x+cos^22x+2sin2x.cos2x}{cos^22x-sin^22x}=\frac{\left(cos2x+sin2x\right)^2}{\left(cos2x-sin2x\right)\left(cos2x+sin2x\right)}\)
\(=\frac{cos2x+sin2x}{cos2x-sin2x}=\frac{1+\frac{sin2x}{cos2x}}{1-\frac{sin2x}{cos2x}}=\frac{1+tan2x}{1-tan2x}\)
CM
1 tháng 6 2017
Chọn A
Ta có: - sin 3 x + cos 3 x = sin x – cos x
⇔ ( c os x- sin x) . ( c os 2 x + c osx. sin x+sin 2 x ) + ( c os x - sin x) = 0 ⇔ ( c os x- sin x) . ( 1 + c osx. sin x ) + ( c os x - sin x) = 0 ⇔ ( c osx - sin x ). (1+ c os x. sinx + 1 ) = 0 ⇔ ( c osx - sin x ). (2+ sin 2 x 2 ) = 0 ⇔ cosx - sinx = 0 sin 2 x 2 = − 2
cosx - sin x =0 ⇔ 2 cos x + π 4 = 0 ⇔ cos x + π 4 = 0 ⇔ x + π 4 = π 2 + k π ⇔ x = π 4 + k π
sin 2 x 2 = − 2 ⇔ sin 2 x = − 4 < − 1 n ê n l o ạ i
Vậy nghiệm của phương trình đã cho là: x = π 4 + k π
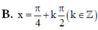
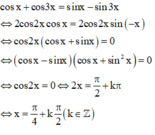
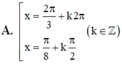
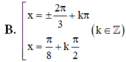
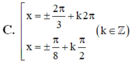
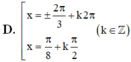
ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)