B={x;y;z}
Hỏi tập hợp B có bao nhiêu tập hợp con
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
3 tháng 4 2017
1) x - 2 = -6
x = -6 + 2
x = -4
2) -5 . x - ( -3 ) =13
-5 . x = 13 + ( -3 )
-5 . x = 10
x = 10 : ( -5 )
x = -2
4 tháng 12 2021
\(\left(a+b\right)\times c=a\times c+b\times c\)
\(a\times\left(b+c\right)=a\times b+a\times c\)
\(a\times\left(b-c\right)=a\times b-a\times c\)
\(a\times b-a\times c=a\times\left(b-c\right)\)
4 tháng 12 2021
( a+b)xc------axc+bxc
a x ( b + c)----- a x b + a x c
a x ( b-c )------ a x b - a x c
a x b-a x c-------a x ( b - c )
ND
1
MQ
1
M
5 tháng 2 2020
\(ĐKXĐ:x\ne\pm1\)
Ta có : \(\frac{x+1}{x^2+x+1}-\frac{x-1}{x^2-x+1}=\frac{2\left(x+2\right)^2}{x^6-1}\)
\(\Leftrightarrow\frac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\frac{2\left(x+2\right)^2}{\left(x^3+1\right)\left(x^3-1\right)}\)
\(\Leftrightarrow\frac{x^3+1-x^3+1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}-\frac{2\left(x+2\right)^2}{\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)}=0\)
\(\Leftrightarrow\frac{2}{\left(x^2+x+1\right)\left(x^2-x+1\right)}-\frac{2\left(x+2\right)^2}{\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)}=0\)
\(\Leftrightarrow\frac{2\left(x+1\right)\left(x-1\right)-2\left(x+2\right)^2}{\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)}=0\)
\(\Leftrightarrow2\left(x^2-1\right)-2\left(x^2+4x+4\right)=0\)
\(\Leftrightarrow2x^2-2-2x^2-8x-8=0\)
\(\Leftrightarrow-8x-10=0\)
\(\Leftrightarrow x=-\frac{5}{4}\)
Vậy \(x=-\frac{5}{4}\) là nghiệm của phương trình.
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 2 2020
a/ \(f\left(x\right)\ge2\sqrt{\frac{16x^2}{x^2}}=8\)
Dấu "=" xảy ra khi \(x^2=\frac{16}{x^2}\Leftrightarrow x=\pm2\)
b/ Hàm này không tồn tại GTNN
c/ \(f\left(x\right)=x+3+\frac{25}{x+3}-4\ge2\sqrt{\frac{25\left(x+3\right)}{x+3}}-4=6\)
Dấu "=" xảy ra khi \(x+3=\frac{25}{x+3}\Leftrightarrow x=2\)
d/ \(f\left(x\right)=x+\frac{9}{x}+3\ge2\sqrt{\frac{9x}{x}}+3=9\)
Dấu "=" xảy ra khi \(x=\frac{9}{x}\Leftrightarrow x=3\)
NY
1
14 tháng 7 2021
bn này bị j rùi mọi người!đây mà là toán lớp 3!
CM
18 tháng 6 2019
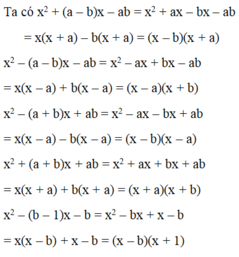
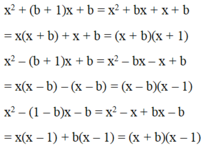
T = [ x 2 + ( a − b ) x − a b x 2 − ( a − b ) x − a b . x 2 − ( a + b ) x + a b x 2 + ( a + b ) x + a b ] : [ x 2 − ( b − 1 ) x − b x 2 + ( b + 1 ) x + b . x 2 − ( b + 1 ) x + b x 2 − ( 1 − b ) x − b ] = [ ( x − b ) ( x + a ) ( x − a ) ( x + b ) . ( x − a ) ( x − b ) ( x + a ) ( x + b ) ] : [ ( x − b ) ( x + 1 ) ( x + b ) ( x + 1 ) . ( x − 1 ) ( x − b ) ( x + b ) ( x − 1 ) ] = ( x − b ) 2 ( x + b ) 2 : ( x − b ) 2 ( x + b ) 2 = 1
Vậy T = 1
Đáp án cần chọn là: A
Tập hợp B có: 23 = 8 tập con