Bài 1:Cho hbh ABCD . Gọi E,F,I là TĐ của AD,CB,CD . Gọi M là điểm đối xứng của I qua E a)Cm : AIDN là hbhb) Gọi N là điểm đối xứng của I qua F . Cm: BICN là hbhc)Gọi H là TĐ của AB . Cm: H là TĐ của MNBài 2:Cho hcn ABCD có AB=4cm,AD=3cm . Gọi E là TĐ của AD . Vẽ EF vuông góc CD tại Fa)Cm:AEFD và BCFE là hcnb)EF cắt BD tại H . Gọi I là TĐ của ADCm:DHEI là hbhc)AIHE là hình gì ? Vì sao ?d)Tính diện tích các hình sau : ABCD,ABD,AIHE,IEC ...
Đọc tiếp
Bài 1:Cho hbh ABCD . Gọi E,F,I là TĐ của AD,CB,CD . Gọi M là điểm đối xứng của I qua E
a)Cm : AIDN là hbh
b) Gọi N là điểm đối xứng của I qua F . Cm: BICN là hbh
c)Gọi H là TĐ của AB . Cm: H là TĐ của MN
Bài 2:Cho hcn ABCD có AB=4cm,AD=3cm . Gọi E là TĐ của AD . Vẽ EF vuông góc CD tại F
a)Cm:AEFD và BCFE là hcn
b)EF cắt BD tại H . Gọi I là TĐ của AD
Cm:DHEI là hbh
c)AIHE là hình gì ? Vì sao ?
d)Tính diện tích các hình sau : ABCD,ABD,AIHE,IEC
~Hết~
Giải giúp mk nhé ! Mk đang cần
C.ơn
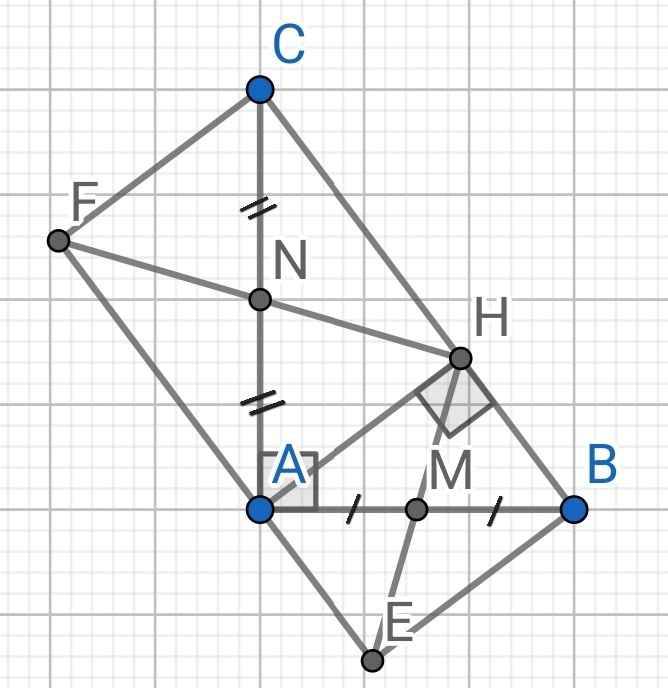
Bài 1
a/ AB // DI
Mà AM thuộc tia AB => AM // DI (1)
=> Tứ giác AIDM là hình thang
E là trung điểm của AD (gt) => ED = EA
Xét △EDI và △EAM có:
- Góc DEI = Góc AEM (đối đỉnh)
- ED = EA (cmt)
- Góc EDI = Góc EAM (slt)
=> △EDI = △EAM (g.c.g)
=> AM = DI (2)
Từ (1) và (2). Vậy: Tứ giác AIDM là hình bình hành (đpcm)
b/ Chứng minh tương tự câu a
c/ Hình bình hành BICN có: BN = IC = CD/2 (I là trung điểm của CD)
Hình bình hành AIDM có: MA = ID = CD/2 (I là trung điểm của CD)
=> BN = MA (3)
Mặt khác ta có: H là trung điểm của AB (gt) hay HA = HB (4)
Từ (3) và (4) suy ra: BN + HA = HB + MA
Hay: HM = HN
Hay: H là trung điểm của MN (đpcm
Bài 2: Đề sai nên không thể giải
c.ơn nha