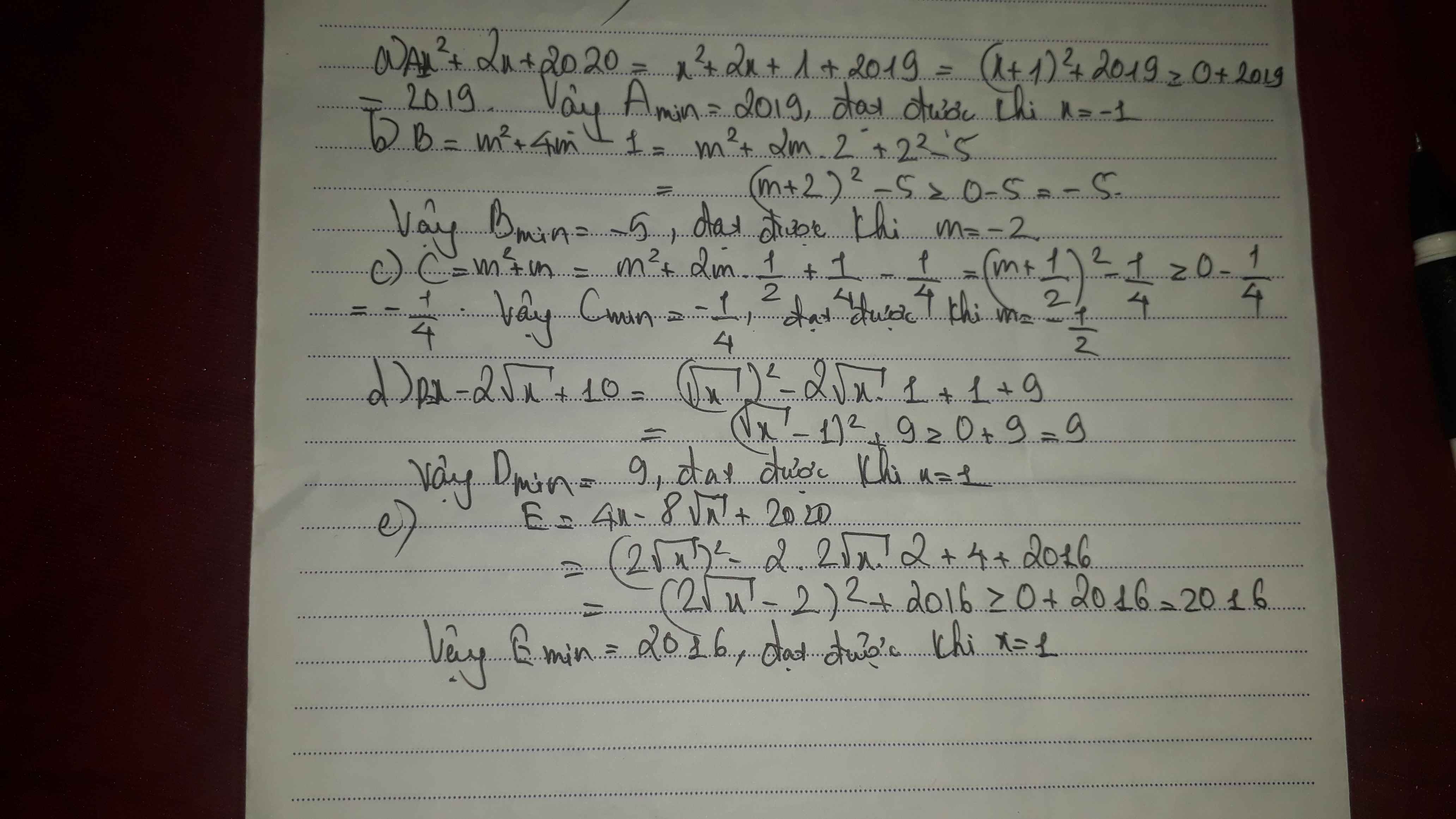Tìm GTNN , GTLN của A= 1/ (5 + 2căn (6-x2))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2019
\(A=2\sqrt{x-1}+\sqrt{10-4x}\)
\(=\sqrt{4x-4}+\sqrt{10-4x}\)
Áp dung BĐT Bun-hia-cop-xki:
\(|\sqrt{4x-4}+\sqrt{10-4x}|\le\sqrt{1+1}.\sqrt{4x-4+10-4x}=2\sqrt{3}\)
\(\Rightarrow-2\sqrt{3}\le A\le2\sqrt{3}\)
Dấu '=' xảy ra khi \(x=\frac{7}{4}\)
28 tháng 7 2023
1:
a: =x^2-7x+49/4-5/4
=(x-7/2)^2-5/4>=-5/4
Dấu = xảy ra khi x=7/2
b: =x^2+x+1/4-13/4
=(x+1/2)^2-13/4>=-13/4
Dấu = xảy ra khi x=-1/2
e: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=1/2
f: x^2-4x+7
=x^2-4x+4+3
=(x-2)^2+3>=3
Dấu = xảy ra khi x=2
2:
a: A=2x^2+4x+9
=2x^2+4x+2+7
=2(x^2+2x+1)+7
=2(x+1)^2+7>=7
Dấu = xảy ra khi x=-1
b: x^2+2x+4
=x^2+2x+1+3
=(x+1)^2+3>=3
Dấu = xảy ra khi x=-1
NH
1
31 tháng 5 2023
A=3(x^2+2/3x-1)
=3(x^2+2*x*1/3+1/9-10/9)
=3(x+1/3)^2-10/3>=-10/3
Dấu = xảy ra khi x=-1/3
\(B=1+\dfrac{15}{x^2+x+5}=1+\dfrac{15}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}}< =1+15:\dfrac{19}{4}=1+\dfrac{60}{19}=\dfrac{79}{19}\)
Dấu = xảy ra khi x=-1/2
QA
0
MT
3
26 tháng 7 2021
\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1
b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2
c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)
dấu"=" xảy ra<=>x=1
b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)
dấu"=" xảy ra<=>x=1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(A=\dfrac{-x^2-1+x^2+4x+4}{x^2+1}=-1+\dfrac{\left(x+2\right)^2}{x^2+1}\ge-1\)
\(A_{min}=-1\) khi \(x=-2\)
\(A=\dfrac{4x^2+4-4x^2+4x-1}{x^2+1}=4-\dfrac{\left(2x-1\right)^2}{x^2+1}\le4\)
\(A_{max}=4\) khi \(x=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(A=\dfrac{-x^2-1+x^2-4x+4}{x^2+1}=-1+\dfrac{\left(x-2\right)^2}{x^2+1}\ge-1\)
\(A_{min}=-1\) khi \(x=2\)
\(A=\dfrac{4x^2+4-4x^2-4x-1}{x^2+1}=4-\dfrac{\left(2x+1\right)^2}{x^2+1}\le4\)
\(A_{max}=4\) khi \(x=-\dfrac{1}{2}\)
VP
2
2 tháng 5 2017
3A=3(x^2-x+1)/(x^2+x+1)
3A-1=(3x^2-3x+3)/(x^2+x+1)-1
3A-1=(3x^2-3x+3-x^2-x-1)/(x^2+x+1)
3A-1=(2x^2-4x+2)/(x^2+x+1)
3A-1=2(x-1)^2/(x^2+x+1)>=0
=>3A>=1
A>=1/3
=>GTNN của A là 1/3 khi x-1=0 hay x=1
A-3=(x^2-x+1)/(x^2+x+1)-3
A-3=(x^2-x+1-3x^2-3x-3)/(x^2+x+1)
A-3=(-2x^2-4x-2)/(x^2+x+1)
A-3=-2(x+1)^2/(x^2+x+1)<=0
=>A<=3
=>GTLN của A=3 khi x=-1
Z
QA
5 tháng 2 2022
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1