cho tứ giác ABCD.Gọi O là giao điểm của hai đường chéo AC và BD.
a)Chứng minh:AB+BC+CD+AD/2<OA+OB+OC+OD<AB+BC+CD+AD
b)Khi O là điểm bất kì trong tứ giác ABCD,kết luận trên có đúng không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 7 2023
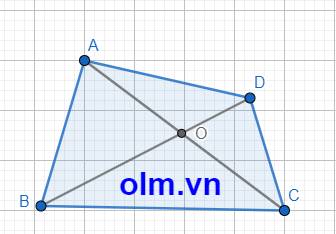
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD
19 tháng 7 2016
Gọi O là giao điểm hai đường chéo AC và BD
- Xét lần lượt các tam giác OAB , OBC , OCD , OAD và áp dụng bất đẳng thức tam giác được :
\(OA+OB>AB\) ; \(OB+OC>BC\) ; \(OC+OD>CD\) ; \(OA+OD>AD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(OA+OB+OC+OD\right)>AB+BC+CD+AD\)
\(\Rightarrow2\left(AC+BD\right)>AB+BC+CD+AD\) \(\Rightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\) (1)
- Tương tự, lần lượt xét các tam giác ACD , BCD , BAC , ABD và áp dụng bất đẳng thức tam giác được :
\(AD+CD>AC\) ; \(BC+CD>BD\) ; \(AB+BC>AC\) ; \(AB+AD>BD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Rightarrow AC+BD< AB+BC+CD+DA\)(2)
Từ (1) và (2) ta có : \(\frac{AB+BC+CD+DA}{2}< AC+BD< AB+BC+CD+AD\)
hay \(\frac{AB+BC+CD+DA}{2}< OA+OB+OC+OD< AB+BC+CD+AD\)
21 tháng 11 2021
Đáp án: Giải thích các bước giải a) Hình bình hành ABCD gọi OO là giao điểm của AC và BD ⇒O⇒O là trung điểm của AC, BD (tính chất ) Xét hai tam giác vuông ΔOEBΔOEB và OFDOFD có: OB=ODOB=OD ˆBOE=ˆDOFBOE^=DOF^ (đối đỉnh) ⇒ΔOEB=ΔOFD⇒ΔOEB=ΔOFD (cạnh huyền-góc nhọn) ⇒BE=DF⇒BE=DF (hai cạnh tương ứng) Và có BE//DFBE//DF (vì cùng vuông góc với AC giả thiết) Từ hai điều trên ⇒⇒ tứ giác BEDF là hình bình hành (dấu hiệu nhận biết) b) Xét ΔHBCΔHBC và ΔKDCΔKDC có: ˆBHC=ˆDKC=90oBHC^=DKC^=90o (giả thiết) ˆHBC=ˆKDCHBC^=KDC^ (=ˆBAD=BAD^ đồng vị) ⇒ΔHBC∼ΔKDC⇒ΔHBC∼ΔKDC (g.g) ⇒CHCK=CBCD⇒CHCK=CBCD (hai cạnh tương ứng tỉ lệ) ⇒CH.CD=CK.CB⇒CH.CD=CK.CB (đpcm) c) Xét ΔAEBΔAEB và ΔAHCΔAHC có: ˆAA^ chung ˆAEB=ˆAHC=90oAEB^=AHC^=90o ⇒ΔAEB∼ΔAHC⇒ΔAEB∼ΔAHC (g.g) ⇒AEAH=ABAC⇒AEAH=ABAC (hai cạnh tương ứng tỉ lệ) ⇒AE.AC=AB.AH⇒AE.AC=AB.AH (1) Xét ΔAFDΔAFD và ΔAKCΔAKC có: ˆAA^ chung ˆAFD=ˆAKC=90oAFD^=AKC^=90o ⇒ΔAFD=ΔAKC⇒ΔAFD=ΔAKC (g.g) ⇒AFAK=ADAC⇒AFAK=ADAC (hai cạnh tương ứng bằng nhau) ⇒AF.AC=AK.AD⇒AF.AC=AK.AD (2) Ta có OE=OF (suy ra từ ΔOEB=ΔOFDΔOEB=ΔOFD câu a) OA=OC (tính chất hình bình hành) ⇒OA−OE=OC−OF⇒OA−OE=OC−OF hay AE=FCAE=FC (3) Từ (1), (2) và (3) suy ra AB.AH+AK.AD=AE.AC+AF.ACAB.AH+AK.AD=AE.AC+AF.AC =AC(AE+AF)=AC(FC+AF)=AC2=AC(AE+AF)=AC(FC+AF)=AC2 (đpcm)
27 tháng 9 2019
Theo bất đẳng thức tam giác ta có:
\(OA+OB>AB\)
\(OB+OC>BC\)
\(OC+OD>DC\)
\(OD+OA>AD\)
Cộng vế theo vế thì \(2\left(OA+OB+OC+OD\right)>AB+BC+CA+AD\)
\(\Rightarrow OA+OB+OC+OD>\frac{AB+BC+CA+AD}{2}\) ( 1 )
Theo bất đẳng thức tam giác ta có:
\(AB+BC>CA;BC+CD>BD;CD+DA>CA;DA+AB>BD\)
Cộng vế theo vế ta có:
\(2\left(AB+BC+CD+AD\right)>2\left(CA+BD\right)=2\left(AO+OC+OD+OB\right)\)
\(\Leftrightarrow AB+BC+CD+DA>OA+OB+OC+OD\) ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra đpcm.
P
21 tháng 7 2023
a)
Ta có
OA + OB > AB ( Bất đẳng thức tam giác )
OC + OD > CD ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OB + OC +OD > AB + CD
=> AC + BD > AB + CD
Bài toán được chứng minh
b)
Ta có:
OA + OD > AD ( Bất đẳng thức tam giác )
OC + OB > CB ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OD + OC + OB > AD + CB
=> AC + BD > AD + BC
Bài toán được chứng minh
18 tháng 4 2022
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔOAB\(\sim\)ΔOCD
b: Xét hình thang ABCD có HK//AB//CD
nên AH/AD=BK/BC(1)
Xét ΔADC có OH//DC
nên OH/DC=AH/AD(2)
Xét ΔBDC có OK//DC
nên OK/DC=BK/BC(3)
Từ (1), (2) và (3) suy ra OH=OK
hay O là trung điểm của HK