K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 7 2023
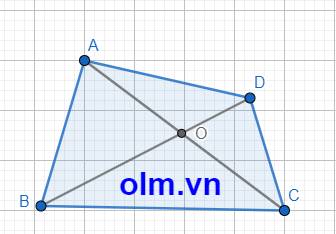
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD

a)
Ta có
OA + OB > AB ( Bất đẳng thức tam giác )
OC + OD > CD ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OB + OC +OD > AB + CD
=> AC + BD > AB + CD
Bài toán được chứng minh
b)
Ta có:
OA + OD > AD ( Bất đẳng thức tam giác )
OC + OB > CB ( Bất đẳng thức tam giác )
Công dọc theo vế:
=> OA + OD + OC + OB > AD + CB
=> AC + BD > AD + BC
Bài toán được chứng minh