Cho tam giác ABC , trên cạnh AB lấy D sao cho AD=2BD . Từ D kẻ DE song song với BC ( E thuộc AC ) .Từ E kẻ EK song song với AB, K thuộc BC
Nêu các cặp tam giác đồng dạng, các cặp góc tương ứng bằng nhau, tỉ số đồng dạng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 3 2023
a: ΔADE đồng dạng với ΔABC
góc ADE=góc ABC, góc AED=góc ACB
k=AD/AB=2/5
b: DE//BC
=>AD/AB=DE/BC
=>DE/6,5=2/5
=>DE=2,6cm
H9
HT.Phong (9A5)
CTVHS
1 tháng 3 2023
Bài này là: Bài 27 trang 72 Toán 8 Tập 2 đúng không bạn
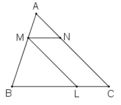
a) \(\Delta ABC\) có \(MN\) // \(BC\) \(\left(M\in AB;N\in AC\right)\Rightarrow\Delta AMN\sim\Delta ABC\) (định lí)
\(\Delta ABC\) có \(ML\) // \(AC\) \(\left(M\in AB;L\in BC\right)\Rightarrow\Delta MBL\sim\Delta ABC\) (định lí)
Vì \(\Delta AMN\sim\Delta ABC\) và \(\Delta MBL\sim\Delta ABC\)
\(\Rightarrow\Delta AMN\sim\Delta MBL\)
b) Xét \(\Delta AMN\sim\Delta ABC\) có:
\(\widehat{A}\) chung
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{C}\)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)
Tỉ số đồng dạng : \(k=\dfrac{AM}{AB}=\dfrac{1}{2}\left(AM=\dfrac{1}{2}MB\right)\)
Xét \(\Delta MBL\sim\Delta ABC\) có:
\(\widehat{B}\) chung
\(\widehat{BML}=\widehat{A};\widehat{MLK}=\widehat{C}\)
\(\dfrac{BM}{BA}=\dfrac{BL}{BC}=\dfrac{ML}{AC}\)
Tỉ số đồng dạng: \(k'=\dfrac{BM}{BA}=\dfrac{2}{3}\)
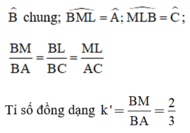
Xét \(\Delta AMN\sim\Delta MBL\) có:
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{BLM};\widehat{A}=\widehat{BML}\)
\(\dfrac{AM}{MB}=\dfrac{AN}{ML}=\dfrac{MN}{BL}\)
Tỉ số đồng dạng: \(k''=\dfrac{AM}{MB}=\dfrac{1}{2}\)
CM
26 tháng 10 2017
a) ΔABC có MN // BC (M ∈ AB; N ∈ AC) ⇒ ΔAMN 
ΔABC.
ΔABC có ML // AC (M ∈ AB; L ∈ BC) ⇒ ΔMBL 
ΔABC
ΔAMN 
ΔABC; ΔMBL 
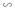ΔABC ⇒ ΔAMN 
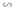ΔMBL.
b) ΔAMN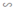 
ΔABC có:
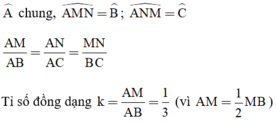
ΔMBL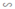 
ΔABC có:
ΔAMN 
ΔMBL có:
3 tháng 3 2023
a: ΔCEF đồng dạng với ΔCAB theo tỉ số k=CE/CA
ΔADE đồng dạng với ΔABC
=>k'=AD/AB=2/5
b: \(\dfrac{C_{ADE}}{C_{ABC}}=\dfrac{AD}{AB}=\dfrac{2}{5}\)
=>\(C_{ADE}=\dfrac{2}{5}\cdot\left(5+7+9\right)=\dfrac{2}{5}\cdot21=\dfrac{42}{5}\left(cm\right)\)
ΔCEF đồng dạng với ΔCAB
=>\(\dfrac{C_{CEF}}{C_{CAB}}=\dfrac{CE}{CA}=\dfrac{3}{5}\)
=>\(C_{CEF}=\dfrac{3}{5}\cdot\left(5+7+9\right)=\dfrac{3}{5}\cdot21=\dfrac{63}{5}\left(cm\right)\)
27 tháng 6 2023
a: Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=3/5
=>DE=6cm
b: Xét ΔADE và ΔCGE có
góc AED=góc CEG
góc EAD=góc ECG
=>ΔADE đồng dạng với ΔCGE
c: Xét tứ giác DBCG có
DG//BC
DB//CG
=>DBCG là hình bình hành
=>DB=CG
HH
23 tháng 3 2020
a, Tam giác ABC có MN // BC \(\left(M\in AB;N\in AC\right)\)=> Tam giác AMN 
tam giác ABC
Tam giác ABC có ML // AC \(\left(M\in AB;L\in BC\right)\)=> Tam giác MBL tam giác ABC
Tam giác AMN tam giác ABC ; tam giác MBL tam giác ABC = >Tam giác AMN MBL
b, Tam giác AMN tam giác ABC , ta có :
\(\widehat{A} chung ,\widehat{AMN}=\widehat{B} ; \widehat{ANC}=\widehat{C}\)
\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)
Tỉ số đồng dạng \(k=\frac{AM}{AB}=\frac{1}{3}\)( Vì AM = \(\frac{1}{2}\)MB )
Tam giác AMNtam giác ABC có :
\(\widehat{B}\)chung ; \(\widehat{BML}=\widehat{A}\); \(\widehat{MLB}=\widehat{C}\)
\(\frac{BM}{BA}=\frac{BL}{BC}=\frac{ML}{AC}\)
Tỉ số đồng dạng \(k'=\frac{BM}{BA}=\frac{2}{3}\)
Tam giác AMN tam giác MBL , ta có :
\(\widehat{AMN}=\widehat{B};\widehat{ANM}=\widehat{BLM};\widehat{A}=\widehat{BLM}\)
\(\frac{AM}{MB}=\frac{AN}{ML}=\frac{MN}{BL}\)
=> Tiwr số đồng dạng \(k''=\frac{AM}{MB}=\frac{1}{2}\)
1 tháng 7 2023
a: Xét ΔACB và ΔCEK có
góc ACB=góc CEK(=góc AED)
góc BAC=góc KCE
=>ΔACB đồng dạng với ΔCEK
b: Xét ΔHEK và ΔHCB có
góc HEK=góc HCB
góc EHK=góc CHB
=>ΔHEK đồng dạng với ΔHCB
=>EK/CB=HE/HC
=>EK*HC=CB*HE