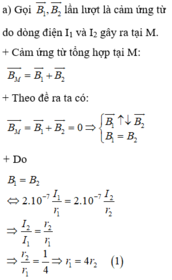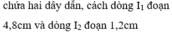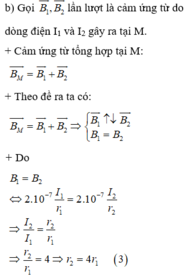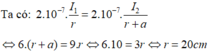Tại sao các tập hợp vô hạn lại không bằng nhau ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
19 tháng 8 2015
bn vào đây xem nhé Chứng minh rằng" có vô số số nguyên tố>? | Yahoo Hỏi & Đáp
12 tháng 11 2016
Giải:
Giả sử số số nguyên tố là hữu hạn thì ta xét số A bằng tích của tất cả các số nguyên tố đó cộng 1. Rõ ràng A nằm ngoài tập hợp các số nguyên tố (vì lớn hơn tất cả các số nguyên tố) nên nó không phải là số nguyên tố. Gọi B là ước số nhỏ nhất của A. Đến lượt B cũng không phải là số nguyên tố vì ta có thể thấy A không chia hết cho số nguyên tố nào (trong tập hợp hữu hạn các số nguyên tố, như đã giả thiết). Vậy B phải chia hết cho một số C. Số C này, dĩ nhiên là ước số của A, và nhỏ hơn B, mâu thuẫn. Tóm lại số số nguyên tố phải là vô hạn.
L
8
LM
6 tháng 10 2021
Trong toán học, một tập hợp là một bộ các phần tử.[1][2][3] Các phần tử tạo nên một tập hợp có thể là bất kỳ loại đối tượng toán học nào: số, ký hiệu, điểm trong không gian, đường thẳng, các hình dạng hình học khác, các biến hoặc thậm chí các tập hợp khác.[4] Tập hợp không có phần tử nào là tập hợp rỗng ; một tập hợp với một phần tử duy nhất là một đơn điểm. Một tập hợp có thể có một số phần tử hữu hạn hoặc là một tập hợp vô hạn. Hai tập hợp bằng nhau khi và chỉ khi chúng có chính xác các phần tử giống nhau.[5]
Tập hợp có mặt khắp nơi trong toán học hiện đại. Thật vậy, lý thuyết tập hợp, cụ thể hơn là lý thuyết tập hợp Zermelo-Fraenkel, đã là phương pháp tiêu chuẩn để cung cấp nền tảng chặt chẽ cho tất cả các phân nhánh của toán học kể từ nửa đầu thế kỷ 20.[4]
^HT^
LM
6 tháng 10 2021
Một tập hợp có thể có một số phần tử hữu hạn hoặc là một tập hợp vô hạn. ... Nghịch lý Cantor cho thấy “tập hợp của tất cả các tập hợp” không thể tồn tại.
^HT^
+
VT
27 tháng 3 2018
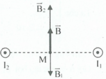
Gọi B 1 → , B 2 → lần lượt là cảm ứng từ do dòng điện I 1 v à I 2 gây ra tại M. Áp dụng quy tắc nắm bàn tay phải xác định được chiều của B 1 → , B 2 → như hình vẽ.
Ta có: B 1 = 2.10 − 7 . I 1 r 1 = 2.10 − 7 . 10 0 , 04 = 5.10 − 5 T B 2 = 2.10 − 7 . I 2 r 2 = 2.10 − 7 . 20 0 , 04 = 10.10 − 5 T
Cảm ứng từ tổng hợp tại M: B → = B 1 → + B 2 →
Vì B 1 → , B 2 → ngược chiều và B 2 > B 1 nên vectơ cảm ứng từ tổng hợp B → có chiều là chiều của B 2 → và có độ lớn : B = B 2 − B 1 = 5.10 − 5 T
Chọn A
CM
26 tháng 8 2017
Vì mỗi hình vuông đều là một hình thoi nên A ⊂ B.
Có những hình thoi không phải là hình vuông nên B ⊄ A.
Vậy A ≠ B.
