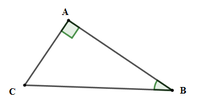
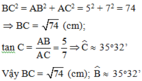CHO TAM GIÁC ABC VUÔNG TẠI A CÓ AC = 5cm

NT

nguyễn thái sơn

19 tháng 5 2018 - olm

CHO TAM GIÁC ABC VUÔNG TẠI A CÓ AC = 5cm ; BC = 13cm A, TÍNH AB VÀ SO SÁNH CÁC GÓC CỦA TAM GIÁC ABC B, TRÊN TIA AC LẤY AD SAO CHO AD = AB . VẼ AE VUÔNG GÓC VỚI BD ( E THUỘC BD ) . CM TAM GIÁC AED = AEB VÀ AE LÀ TIA PHÂN GIÁC CỦA GÓC BADC, AE CẮT BC TẠI F , CM GÓC ADF = ABFD, ĐƯỜNG THẲNG VUÔNG GÓC VỚI BC TẠI F CẮT TIA CD TẠI H . CM FB = FH MIK CẦN GẤP , BẠN NÀO LÀM ĐƯỢC MIK CẢM ƠN TRƯỚC NHÉ + HÌNH LUÔN...

Đọc tiếp

#Toán lớp 7

1

TT

Trần Thị Kiều Trâm

19 tháng 5 2018

Đúng(0)

NN

Như Nguyễn

13 tháng 12 2023

Cho ∆ABC vuông tại A. a) Biết AC = 5cm, AC = 12cm. Giải tam giác vuông ABC. b) Biết AC = 5cm, góc B = 40°. Giải tam giác vuông ABC

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 12 2023

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=5^2+12^2=169\)

=>\(BC=\sqrt{169}=13\left(cm\right)\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{5}{13}\)

nên \(\widehat{B}\simeq23^0\)

Ta có: ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{C}\simeq90^0-23^0=67^0\)

b: Ta có: ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{C}=90^0-40^0=50^0\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)

=>\(BC=\dfrac{AC}{sinB}=\dfrac{5}{sin40}\simeq7,78\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB^2=BC^2-AC^2\)

=>\(AB\simeq\sqrt{7,78^2-5^2}\simeq5,96\left(cm\right)\)

Đúng(1)

⊰⊹🅼🅸🅸🅽🅷☠☆

27 tháng 4 2023

cho tam giác abc vuông tại a có ab=3cm ac=5cm đường phân giác ad . đường vuông góc dc cắt ac ở ea, tam giác abc đồng dạng tam giác becb, tính bc, bd,ad

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 4 2023

a:

Sửa đề tam giác DEC

Xet ΔABC vuông tại A và ΔDEC vuông tại D có

góc C chung

=>ΔABC đồng dạng với ΔDEC

b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)

\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)

AD là phân giác

=>BD/AB=CD/AC

=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)

=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)

Đúng(0)

A

Anni

6 tháng 3 2022

. Tam giác ABC có BC = 3cm ; AC = 5cm ; AB = 4cm. Tam giác ABC vuông tại đâu?A. Tại B B. Tại C C. Tại A D. Không phải là tam giác...

Đọc tiếp

#Toán lớp 7

5

SM

Sơn Mai Thanh Hoàng

6 tháng 3 2022

A

Đúng(2)

TC

TV Cuber

6 tháng 3 2022

A,tại B

Đúng(3)

BB

Big Bang

2 tháng 5 2016 - olm

Cho tam giác ABC có AB = 3 cm; AC = 4 cm; BC=5cm. Chứng tỏ tam giác ABC vuông tại A

#Toán lớp 7

2

KH

Kakashi Hakate

2 tháng 5 2016

Ta có : 3^2+4^2=9+16=25

Căn bậc hai của 25 bằng 5 suy ra tam giac ABC vuong tai A

Đúng(0)

D

Devil

2 tháng 5 2016

ta có:

\(AB^2+AC^2=3^2+4^2=9+16=25\)

\(BC^2=5^2=25\)

=> tam giác ABC vuông tại A

Đúng(0)

NN

nguyễn ngự nhất

10 tháng 4 2016 - olm

cho tam giác ABC có AB=3CM AC= 5CM BC=4CM

a,,CHỨNG tỏ tam giác abc vuông tại b

#Toán lớp 7

1

TN

Trần Nhật Nam

20 tháng 2 2022

Áp dụng đlý Pytago vào tam giác ABC:

AC²=BC²+AB²

5²=4²+3²

5²=25

Vậy tam giác ABC là tam giác vuông tại B (dpcm)

Đúng(0)

PT

Pham Trong Bach

25 tháng 10 2018

Cho tam giác ABC vuông tại A có AC = 7cm, AB = 5cm. Tính BC; C ^ A. B C = 74 ( c m ) ; B ^ ≈ 35 0 32 ' B. B C = 74 ( c m ) ; B ^ ≈ 36 0 32 ' C. B C = 74 ( c m ) ; B ^ ≈ 35 0 33 ' D. B C = 75 ( c m ) ; ...

Đọc tiếp

#Toán lớp 9

1

CM

Cao Minh Tâm

25 tháng 10 2018

Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: A

Đúng(1)

NT

Nguyễn Thu Trang

7 tháng 10 2017 - olm

cho tam giác abc có ab=5cm, ac=12cm,bc=13cm
a)chứng minh tam giác ABC vuông tại A và tính độ dài đường cao AH
b)kẻ HE vuong AB tại E , HF vuông AC tại F . Chứng minhAE.AB=AF>AC
c)chứng minh tam giác AFE và tanm giác ABC đồng dạng

#Toán lớp 9

0

TA

Trâm Anh Huỳnh

18 tháng 3 2022

Cho tam giác ABC vuông tại A. Có AB=5cm, AC=12cm

a. Tính độ dài BD

b. Trên tia đối của tia AC lấy điểm D sao cho AC=AD. Chứng minh tam giác ABC=tam giácABD

c.Từ A kẻ AE và AF lần lượt vuông góc với BD và BC tại E,F. C/m tam giác AEF cân

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

15 tháng 1

a: Sửa đề: Tính BC

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=5^2+12^2=169\)

=>\(BC=\sqrt{169}=13\left(cm\right)\)

b: Xét ΔABC vuông tại A và ΔABD vuông tại A có

AB chung

AC=AD

Do đó: ΔABC=ΔABD

c: Ta có: ΔABC=ΔABD

=>\(\widehat{ABC}=\widehat{ABD}\)

Xét ΔBEA vuông tại E và ΔBFA vuông tại F có

BA chung

\(\widehat{EBA}=\widehat{FBA}\)

Do đó: ΔBEA=ΔBFA

=>AE=AF

=>ΔAEF cân tại A

Đúng(0)

NM

nguyễn minh thơ

4 tháng 5 2023

cho tam giác ABC vuông tại A có AB=5cm AC=12cm . vẽ đường cao AH a. Chứng minh tam giác HBA đồng dạng tam Giác ABC b tính AH,BH

#Toán lớp 8

1

乇尺尺のﾚ

4 tháng 5 2023

Hình vẽ:

Giải

a. Xét ΔHBA và ΔABC có:

\(\widehat{B}\) chung

\(\widehat{BHA}=\widehat{BAC}=90^0\)

⇒ΔHBA ∼ ΔABC (g.g)

b. Xét ΔABC vuông tại A có:

\(BC^2=AB^2+AC^2\)(định lí py-ta-go)

\(=5^2+12^2\)

\(=169\)

\(\rightarrow BC=\sqrt{169}=13\left(cm\right)\)

Vì ΔABC ∼ ΔHBA (cmt)

\(\rightarrow\dfrac{AB}{BH}=\dfrac{AC}{AH}=\dfrac{BC}{AB}hay\dfrac{5}{BH}=\dfrac{12}{AH}=\dfrac{13}{5}\)

⇒\(BH=\dfrac{5.5}{13}=\dfrac{25}{13}\left(cm\right)\)

⇒\(AH=\dfrac{12.5}{13}=\dfrac{60}{13}\left(cm\right)\)

Đúng(1)

AN

Anh Nguyen

28 tháng 7 2021

Cho tam giác ABC vuông tại A có AC=3cm, AB=4cm, BC=5cm. a)Chứng minh tam giác ABC vuông. Tính góc B và C b) Phân giác của góc A cắt BC tại D. Tính BD và CD.

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 7 2021

a) Xét ΔABC có

\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)

nên ΔABC vuông tại A(Định lí Pytago đảo)

Xét ΔABC vuông tại A có

\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)

\(\Leftrightarrow\widehat{B}=37^0\)

b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)

hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)

mà BD+CD=5

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)

Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP