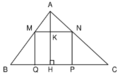
Cho ΔABC có cạnh BC=2y (cm), đường cao AH=y (cm). Vẽ bên trong Δ một hình chữ nhật MNPQ (như hình vẽ) có MQ=x (cm); MN = 4x (cm) với (x>0 ; y>0).a) Viết công thức tính tổng diện tích của tam giác AMN; BMQ và CNP dưới dạng tíchb) Tính tổng diện tích của các tam giác AMN, BMQ, CNP. Biết 2x+y=23; y-2x=7 A B C M N P Q H ...
Đọc tiếp
Cho ΔABC có cạnh BC=2y (cm), đường cao AH=y (cm). Vẽ bên trong Δ một hình chữ nhật MNPQ (như hình vẽ) có MQ=x (cm); MN = 4x (cm) với (x>0 ; y>0).
a) Viết công thức tính tổng diện tích của tam giác AMN; BMQ và CNP dưới dạng tích
b) Tính tổng diện tích của các tam giác AMN, BMQ, CNP. Biết 2x+y=23; y-2x=7
Nè nha bạn.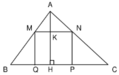
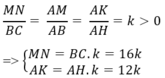
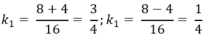
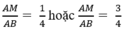
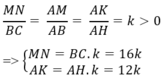
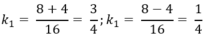
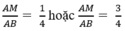
a) Để tính diện tích của tam giác AMN, ta sử dụng công thức diện tích tam giác: Diện tích tam giác = 1/2 * cạnh đáy * chiều cao. Với tam giác AMN, cạnh đáy là MN và chiều cao là AH. Vậy diện tích tam giác AMN là: Diện tích AMN = 1/2 * MN * AH.
b) Để tính tổng diện tích của các tam giác AMN, BMQ và CNP, ta cần tính diện tích của từng tam giác và sau đó cộng chúng lại với nhau. Diện tích tam giác BMQ và CNP cũng được tính bằng công thức diện tích tam giác.
Tuy nhiên, để tính chính xác tổng diện tích của các tam giác, ta cần biết giá trị của x và y. Trong trường hợp này, ta biết rằng 2x + y = 23 và y - 2x = 7. Ta có thể giải hệ phương trình này để tìm giá trị của x và y, sau đó sử dụng giá trị đó để tính tổng diện tích của các tam giác.
Tuy nhiên, để tính chính xác tổng diện tích của các tam giác, ta cần biết giá trị của x và y. Trong trường hợp này, ta biết rằng 2x + y = 23 và y - 2x = 7. Ta có thể giải hệ phương trình này để tìm giá trị của x và y, sau đó sử dụng giá trị đó để tính tổng diện tích của các tam giác.