Cho tam giác DEF cân tại D, đường phân giác DI. Gọi N là trung điểm của IF. Vẽ điểm M sao cho N là trung điểm của DM. CMR:
a, tam giác DIN= tam giác MNF; MF VUÔNG GÓC EF
b, DF>MF
c ,góc IDN=NDF
d, D,I,K thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔDIN và ΔMFN có
ND=NM
\(\widehat{DNM}=\widehat{MNF}\)
NI=NF
Do đó: ΔDIN=ΔMFN
Suy ra: DI=FM
mà DI<DF
nên FM<DF
2: EF=12cm nên IF=6cm
\(\Leftrightarrow DI=FM=\sqrt{8^2-6^2}=2\sqrt{7}\left(cm\right)\)

tự kẻ hình nha:333
a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)
xét tam giác MAB và tam giác DAB có
MH=HD(cmt)
AHM=AHD(=90 độ)
AH chung
=> tam giác MAB= tam giác DAB(cgc)
=> AM=AD( hai cạnh tương ứng)
vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)
xét tam giác AKD và tam giác AKN có
DK=NK(cmt)
AKD=AKN(=90 độ)
AK chung
=> tam giác AKD= tam giác AKN( cgc)
=> AN=AD ( hai cạnh tương ứng)
AM=AD(cmt)
=> AM=AN=> tam giác AMN cân A
b) vì E thuộc đường trung trực AB=> EM=ED
vì F thuộc đường trung trực AC=> FD=FN
ta có MN=ME+EF+FN mà EM=ED, FD=FN
=> MN= ED+EF+FD
c) xét tam giác ADF và tam giác ANF có
FD=FN(cmt)
AD=AN(cmt)
AF chung
=> tam giác ADF= tam giác ANF(ccc)
=> ANF=ADF( hai góc tương ứng)
xét tam giác AME và tam giác ADE có
AM=AD(cmt)
AE chung
EM=ED(cmt)
=> tam giác AME= tam giác ADE(ccc)
=> AME=ADE( hai góc tương ứng)
mà AME=ANF( tam giác AMN cân A)
=> ADE=ADF=> AD là p/g của EDF
d) chưa nghĩ đc :)))))))

Đức Thuận Trần : Bài không hề cho \(\widehat{DIN}=90^o\) hay ΔDIF vuông :))

a: Xét ΔAMD vuông tại M và ΔAMI vuông tại M có
AM chung
MD=MI
Do đó:ΔAMD=ΔAMI
Xét ΔAND vuông tại N và ΔANK vuông tại N có
AN chung
ND=NK
Do đó: ΔAND=ΔANK
b: \(\widehat{IAK}=2\cdot\left(\widehat{DAM}+\widehat{DAN}\right)=2\cdot90^0=180^0\)
=>I,A,K thẳng hàng
c: Ta có: I,A,K thẳng hàng
mà AI=AK(=AD)
nên A là trung điểm của KI

a) xét tam giác DHE và tam giác DHF có
DH chung
DE = DF (gt)
góc DHE = góc DHF (=90 độ)
=> tam giác DHE = tam giác DHF (c.g.c)
=> HE = HF
=> H là trung điểm của EF
b) xét tam giác EMH và tam giác FNH có
HE = HF (cmt)
Góc MEH = góc MFH (gt)
Góc EHM = góc FHM (đối đỉnh)
=> tam giác EMH = tam giác FNH (g.c.g)
=> HM = HN
=> tam giác HMN cân tại H
a: Xét ΔDEH vuông tại H và ΔDFH vuông tại H có
DE=DF
DH chung
=>ΔDEH=ΔDFH
=>EH=FH
=>H là trung điểm của EF
b: Xet ΔDMH và ΔDNH có
DM=DN
góc MDH=góc NDH
DH chung
=>ΔDMH=ΔDNH
=>HM=NH
c: Xet ΔDEF có DM/DE=DN/DF
nên MN//EF
d: ΔDMN cân tại D
mà DI là trug tuyến
nên DI là phân giác của góc EDF
=>D,I,H thẳng hàng

a) Xét ΔDIN và ΔMNF có
DN=MN(N là trung điểm của DM)
\(\widehat{DNI}=\widehat{MNF}\)(hai góc đối đỉnh)
IN=NF(N là trung điểm của IF)
Do đó: ΔDIN=ΔMNF(c-g-c)
⇒\(\widehat{IDN}=\widehat{NMF}\)(hai góc tương ứng)
mà \(\widehat{IDN}\) và \(\widehat{NMF}\) là hai góc ở vị trí so le trong
nên DI//MF(dấu hiệu nhận biết hai đường thẳng song song)
Xét ΔEDI và ΔFDI có
DE=DF(ΔDEF cân tại D)
\(\widehat{EDI}=\widehat{FDI}\)(DI là tia phân giác của \(\widehat{EDF}\))
DI chung
Do đó: ΔEDI=ΔFDI(c-g-c)
⇒\(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\frac{180^0}{2}=90^0\)
⇒DI⊥EF
Ta có: DI⊥EF(cmt)
DI//FM(cmt)
Do đó: FM⊥EF(định lí 2 từ vuông góc tới song song)
b) Xét ΔIFM vuông tại F có IM là cạnh huyền
nên IM là cạnh lớn nhất trong ΔIFM(trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
⇒IM>FM(1)
Xét ΔINM và ΔFND có
IN=FN(N là trung điểm của IF)
\(\widehat{INM}=\widehat{FND}\)(hai góc đối đỉnh)
NM=ND(N là trung điểm của MD)
Do đó: ΔINM=ΔFND(c-g-c)
⇒IM=FD(hai cạnh tương ứng)(2)
Từ (1) và (2) suy ra DF>MF(đpcm)
c) Xét ΔDFM có DF>MF(cmt)
mà góc đối diện với cạnh DF là \(\widehat{DMF}\)
và góc đối diện với cạnh MF là \(\widehat{FDM}\)
nên \(\widehat{DMF}>\widehat{FDM}\)(định lí 1 về quan hệ giữa cạnh và góc đối diện trong tam giác)
mà \(\widehat{DMF}=\widehat{IDN}\)(cmt)
nên \(\widehat{IDN}>\widehat{MDF}\)
hay \(\widehat{IDN}>\widehat{NDF}\)(đpcm)
d) Ta có: ΔEFM vuông tại F(EF⊥FM)
mà FK là đường trung tuyến ứng với cạnh huyền EM(K là trung điểm của EM)
nên \(FK=\frac{EM}{2}\)(định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(EK=\frac{EM}{2}\)(K là trung điểm của EM)
nên FK=EK
⇔K nằm trên đường trung trực của FE(tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: DE=DF(ΔDEF cân tại D)
nên D nằm trên đường trung trực của FE(tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: IE=IF(ΔEDI=ΔFDI)
nên I nằm trên đường trung trực của FE(tính chất đường trung trực của một đoạn thẳng)(5)
Từ (3), (4) và (5) suy ra D,I,K thẳng hàng(đpcm)
Ý C là ghi sai đề bài rồi nhé
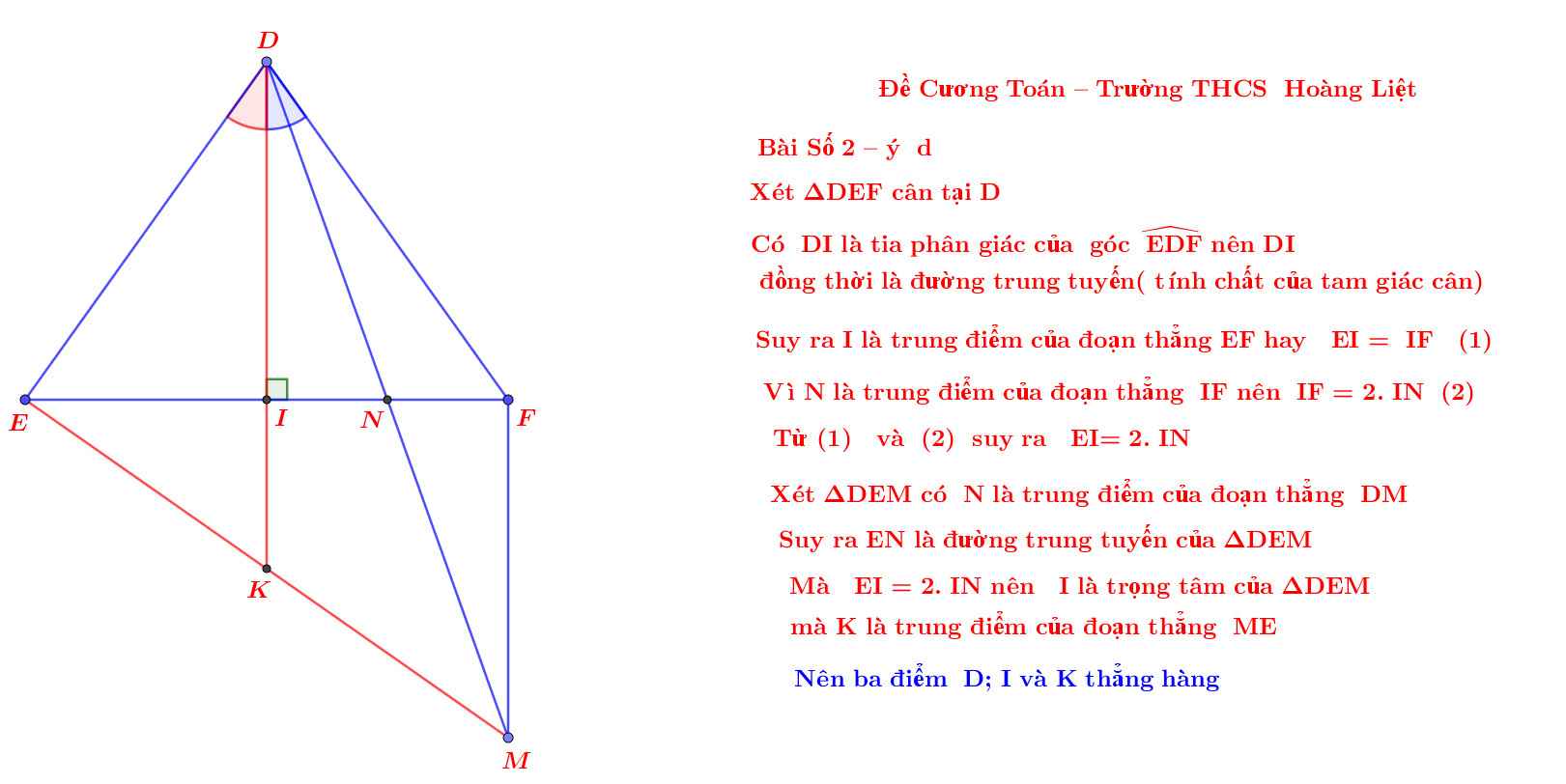
Còn ý d khó nhất thì giải như sau