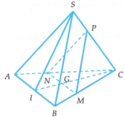
Cho tam giác ABC có G là trọng tâm, lấyP trên BC các đường thẳng đi qua P và song song với CG;BG cắt AB;AC ở E;F đường thẳng EF cắt BG;CG lần lượt tại I và K. CMR
a) EI=IK=KF
b) PQ đi qua trung điểm của EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2017
Ta có: MN II BC => HK\(⊥\)MN
Theo Talet có: \(\frac{HK}{AH}=\frac{GD}{AD}=\frac{1}{3}\)
và: \(\frac{MG}{BD}=\frac{AG}{AD}=\frac{2}{3}\)(*)
\(\frac{GN}{DC}=\frac{AG}{AD}=\frac{2}{3}\)(**)
tỪ (*) và (**) => \(\frac{MN}{BC}=\frac{2}{3}\)
Vậy diện tích tam giác HMN=\(S_{HMN}=\frac{2}{9}.S_{ABC}=\frac{2.36}{9}=8\)
CM
14 tháng 10 2017
Chọn đáp án D
Ta có
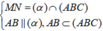
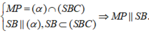
Khi đó 
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
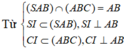
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0
