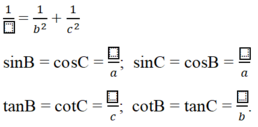Hệ thức lượng trong tam giác vuông
1) biết AH=30cm; AB/AC=5/6
Tính AB, AC,BC,HB,HC
2) biết BC= 125cm; AB/AC= 3/4
Tính HB, HC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AB^2=HB^2+HA^2\)
\(BM\cdot BA=BH^2\)
\(AM\cdot AB=AH^2\)
\(BH\cdot HA=HM\cdot BA\)
\(HM^2=MA\cdot MB\)
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHA vuông tại H có HM là đường cao ứng với cạnh huyền BA, ta được:
\(BM\cdot BA=BH^2\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHC vuông tại H có HN là đường cao ứng với cạnh huyền BC, ta được:
\(BN\cdot BC=BH^2\)
Xét tứ giác BNHM có
\(\widehat{NBM}=\widehat{BNH}=\widehat{BMH}=90^0\)
Do đó: BNHM là hình chữ nhật
Suy ra: BH=NM
Ta có: \(BM\cdot BA+BN\cdot BC\)
\(=BH^2+BH^2\)
\(=2\cdot NM^2\)
Bạn tự vẽ hình nha.
a) \(sinA=\dfrac{BH}{AB},cosA=\dfrac{AH}{AB},tanA=\dfrac{BH}{AH},cotA=\dfrac{AH}{BH}\\sin \widehat{ABH}=\dfrac{AH}{AB},cos\widehat{ABH}=\dfrac{BH}{AB},tan\widehat{ABH}=\dfrac{AH}{BH},cot\widehat{ABH}=\dfrac{BH}{AH}\)
b)Áp dụng định lí Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(CH=\sqrt{BC^2-BH^2}=\sqrt{900-576}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(AC=\dfrac{BC^2}{HC}=\dfrac{900}{18}=50\left(cm\right)\)
\(AB=\dfrac{BH\cdot AC}{BC}=\dfrac{24\cdot50}{30}=40\left(cm\right)\)
\(AH=\dfrac{AB^2}{AC}=\dfrac{400}{50}=8\)(cm)
c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
BN.BC=\(BH^2\)
BM.BA=\(BH^2\)
Suy ra, BN.BC+BM.BA=2\(BH^2\)
Xét tứ giác BMHN có:
góc BMH = góc MBN = góc HNB = \(90^0\)
nên tứ giác BMHN là hình chữ nhật.
suy ra BH = MN .
Suy ra, BN.BC+BM.BA = 2.\(MN^2\)(đpcm)

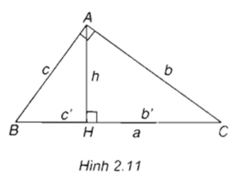
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
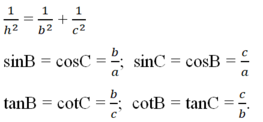

Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

+) Xét tam giác ABC vuông tại A có AH là đường cao => AH là đường trung tuyến của tam giác ABC
=> AH=BH=CH=\(\frac{1}{2}BC\)=6 cm
=> BC=12cm
+) Xét tam giác ABC vuông tại A theo định lí pitago có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow10^2+AC^2=12^2\Leftrightarrow AC=\sqrt{44}\)
Vậy AC=\(\sqrt{44}\)
chúc bn học tốt!

a, \(AB=\sqrt{BC^2-AC^2}=24\left(cm\right)\left(pytago\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=19,2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=10,8\left(cm\right)\\AH=\sqrt{BH\cdot CH}=14,4\left(cm\right)\end{matrix}\right.\)

Xét tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}\)
\(\Rightarrow AB=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AH^2=\dfrac{AC^2AB^2}{AC^2+AB^2}\)
\(\Rightarrow AH=\sqrt{\dfrac{AC^2AB^2}{AC^2+AB^2}}\)
\(\Rightarrow AH=\sqrt{\dfrac{\left(5\sqrt{3}\right)^2\cdot5^2}{\left(5\sqrt{3}\right)^2+5^2}}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Áp dụng hệ thưcs cạnh góc vuông và hình chiếu ta có:
\(\left\{{}\begin{matrix}AB^2=BC\cdot BH\\AC^2=BC\cdot CH\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{5^2}{10}=2,5\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{\left(5\sqrt{3}\right)^2}{10}=7,5\left(cm\right)\end{matrix}\right.\)