Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AB^2=HB^2+HA^2\)
\(BM\cdot BA=BH^2\)
\(AM\cdot AB=AH^2\)
\(BH\cdot HA=HM\cdot BA\)
\(HM^2=MA\cdot MB\)
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHA vuông tại H có HM là đường cao ứng với cạnh huyền BA, ta được:
\(BM\cdot BA=BH^2\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHC vuông tại H có HN là đường cao ứng với cạnh huyền BC, ta được:
\(BN\cdot BC=BH^2\)
Xét tứ giác BNHM có
\(\widehat{NBM}=\widehat{BNH}=\widehat{BMH}=90^0\)
Do đó: BNHM là hình chữ nhật
Suy ra: BH=NM
Ta có: \(BM\cdot BA+BN\cdot BC\)
\(=BH^2+BH^2\)
\(=2\cdot NM^2\)
Bạn tự vẽ hình nha.
a) \(sinA=\dfrac{BH}{AB},cosA=\dfrac{AH}{AB},tanA=\dfrac{BH}{AH},cotA=\dfrac{AH}{BH}\\sin \widehat{ABH}=\dfrac{AH}{AB},cos\widehat{ABH}=\dfrac{BH}{AB},tan\widehat{ABH}=\dfrac{AH}{BH},cot\widehat{ABH}=\dfrac{BH}{AH}\)
b)Áp dụng định lí Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(CH=\sqrt{BC^2-BH^2}=\sqrt{900-576}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(AC=\dfrac{BC^2}{HC}=\dfrac{900}{18}=50\left(cm\right)\)
\(AB=\dfrac{BH\cdot AC}{BC}=\dfrac{24\cdot50}{30}=40\left(cm\right)\)
\(AH=\dfrac{AB^2}{AC}=\dfrac{400}{50}=8\)(cm)
c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
BN.BC=\(BH^2\)
BM.BA=\(BH^2\)
Suy ra, BN.BC+BM.BA=2\(BH^2\)
Xét tứ giác BMHN có:
góc BMH = góc MBN = góc HNB = \(90^0\)
nên tứ giác BMHN là hình chữ nhật.
suy ra BH = MN .
Suy ra, BN.BC+BM.BA = 2.\(MN^2\)(đpcm)

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow AC^2=BC^2-AB^2=10^2-6^2=64\Rightarrow AC=8\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
tam giác AHB vuông tại H có đường cao HD nên áp dụng hệ thức lượng
\(\Rightarrow AD.AB=AH^2\)
tam giác AHC vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=AE.AC\Rightarrow AE.AC=AD.AB\Rightarrow\dfrac{AD}{AE}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\)
b) Vì \(\angle ADH=\angle AEH=\angle DAE=90\Rightarrow ADHE\) là hình chữ nhật
\(\Rightarrow DE=AH\)
Ta có: \(BC.sinB.cosB=BC.\dfrac{AC}{BC}.\dfrac{AB}{BC}=\dfrac{AB.AC}{BC}=AH\)
\(\Rightarrow DE=BC.sinB.cosB\)

a: Xét ΔABC vuông tại A có sin C=AB/BC=3/5
=>cos C=căn 1-(3/5)^2=4/5
=>AC/BC=4/5
=>BC=20(cm)
\(AB=\sqrt{20^2-16^2}=12\left(cm\right)\)
ΔABC vuông tại A có AH là đường cao
nên CH*CB=CA^2
=>CH*20=16^2=256
=>CH=12,8(cm)
b: ΔHAB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔHAC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN đồng dạng với ΔACB

Hệ thức lượng: \(AH^2=BH.CH\)
Hai tam giác vuông BEH và HFC đồng dạng: \(\Rightarrow\dfrac{BE}{FH}=\dfrac{EH}{CF}\Rightarrow BE.CF=EH.FH\)
Hai tam giác vuông AEH và CFH đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{EH}{FH}\Rightarrow AH.FH-CH.EH=0\)
Hai tam giác vuông BEH và AFH đồng dạng \(\Rightarrow\dfrac{BH}{AH}=\dfrac{EH}{FH}\Rightarrow EH.AH-BH.FH=0\)
Ta có: \(\left(BE\sqrt{CH}+CF\sqrt{BH}\right)^2=BE^2.CH+CF^2.BH+2BE.CF.\sqrt{BH.CH}\)
\(=BE^2.CH+CF^2.BH+2BE.CF.AH\)
\(=\left(BH^2-EH^2\right)CH+\left(CH^2-FH^2\right)BH+2BE.CF.AH\)
\(=BH.CH\left(BH+CH\right)-EH^2.CH-FH^2.BH+2EH.FH.AH\)
\(=AH^2.BC+EH\left(AH.FH-EH.CH\right)+FH\left(AH.EH-FH.BH\right)\)
\(=AH^2.BC=\left(AH\sqrt{BC}\right)^2\)
\(\Rightarrow BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)
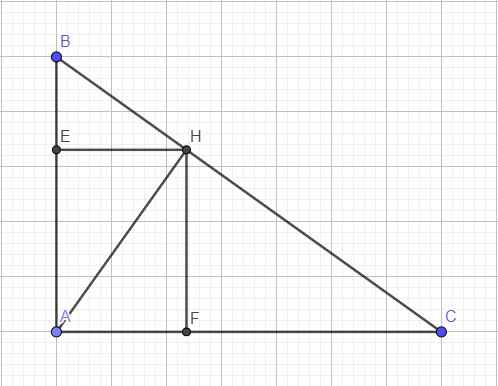
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC