Chứng minh rằng : nếu a + b + c = abc ; \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=2\) thì \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
\(\overline{aba}=101.a+10b=98a+3a+7b+3b=\)
\(=\left(98a+7b\right)+3\left(a+b\right)\)
\(98a+7b⋮7;\left(a+b\right)⋮7\Rightarrow3\left(a+b\right)⋮7\)
\(\Rightarrow\overline{abc}=\left(98a+7b\right)+3\left(a+b\right)⋮7\)
b/ xem lại đề bài

abc=11(a+b+c)
=>100a+10b+c=11a+11b+11c
=> 89a=b+10c
Vì b+10c≤99=) 89a≤99
=> a=1
=> 89=b+10c
=> b=89−10c
Để b không âm và có 1 chữ số => c = 8
=> b=89−80=9
Vậy nếu abc=11(a+b+c) thì a = 1, b = 9, c = 8 (Đpcm)
P/s tham khảo nha

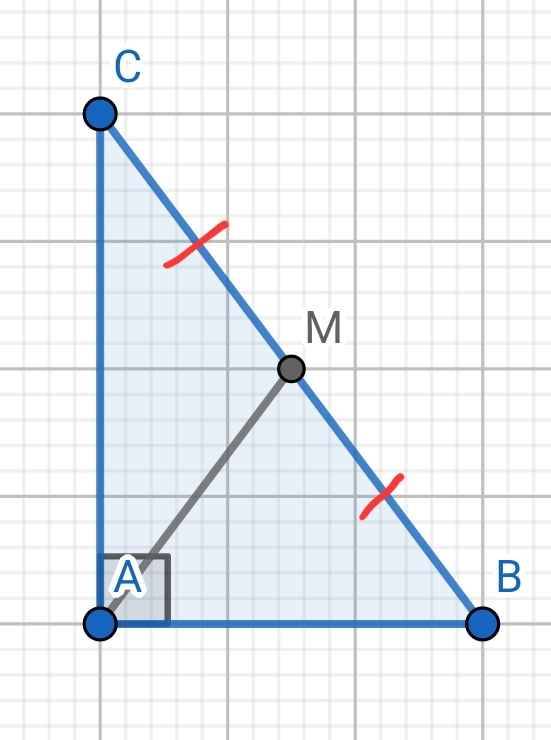
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2

abc = 11 . ( a + b + c )
a . 100 + b . 10 + c = 11 . a + 11 . b + 11 . c
a . 89 = b + 10 . c
a chỉ có thể bằng 1 vì nếu a = 2 thì a . 89 = 198 . Mà b + 10 . c lớn nhất là 98
b + 10 . c = 89
=> b = 9 vì 10 . c có tận cùng là 0
c = ( 89 - 9 ) : 10 = 8
Vậy nếu abc = 11 . ( a + b + c ) thì a = 1 ; b = 9 ; c = 8
b ) ab + ba = 10a + b + 10b + a = 11a + 11b = 11( a + b )
=> ab + ba chia hết cho 11
A ) abc = 11 . ( a + b + c )
a x 100 + b x 10 + c x 1 = 11 . a + 11.b + 11.c
a x 99 = 1.b + b.10
\(\Rightarrow a=1;b=9;c=8\)
B ) ab + ba
= a x 10 + b x 1 + b x 10 + a x 1
= a x ( 10 + 1 ) + b x ( 1 + 10 )
= a x 11 + b x 11
= ( a + b ) x 11
Vì số nào nhân với 11 thì cũng đều chia hết cho 11 nên ( ab + ba ) \(⋮11\)

mk cung dang mac bai nay nen mong nhieu bn giup do chi nha !


\(\dfrac{b^2-a^2}{2c}=b.\dfrac{\left(b^2+c^2-a^2\right)}{2bc}-a.\dfrac{\left(a^2+c^2-b^2\right)}{2ac}\)
\(\Leftrightarrow\dfrac{b^2-a^2}{2c}=\dfrac{b^2+c^2-a^2}{2c}-\dfrac{a^2+c^2-b^2}{2c}\)
\(\Leftrightarrow b^2-a^2=\left(b^2+c^2-a^2\right)-\left(a^2+c^2-b^2\right)\)
\(\Leftrightarrow3b^2=3a^2\Leftrightarrow a=b\)
Hay tam giác cân tại C

\(\Rightarrow100.a+10.b+c=11.a+11.b+11.c\)
\(\Rightarrow89.a=b+10c\Rightarrow a=\frac{b+10.c}{89}\)
Ta có \(b\le9;c\le9\Rightarrow b+10.c\le9+10.9=99\)
Do a là số nguyên => \(b+10.c\)Phải chia hết cho 89 mà \(b+10.c\le99\Rightarrow b+10c=89\Rightarrow a=1\)
Do 10.c là 1 số tròn chục => b + 10.c = 89 có chữ số tận cùng là 9 nên b=9. Thay a=1; b=9 vào biểu thức \(a=\frac{b+10.c}{89}\Rightarrow c=8\)