
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(=\dfrac{1}{7}+\dfrac{3}{4}-\dfrac{8}{7}=\dfrac{3}{4}-1=-\dfrac{1}{4}\)


1000A = 1451,(51)
=> 990A = 1451,(51) - 14,(51)
=> 990A = 1437
=> A = 1437/990 = 479/330

\(\frac{\left(-3\right)^n}{81}=-27\)
=> (-3)n = -27.81
=> (-3)n = -(27.81)
=> (-3)n = -(33.34)
=> (-3)n = -37 = (-3)7
=> n = 7
Vậy n = 7
\(\frac{\left(-3\right)^n}{81}=-27\)
\(\left(-3\right)^n:81=-27\)
\(\left(-3\right)^n=-27\cdot81\)
\(\left(-3\right)^n=-2187\)
\(\left(-3\right)^n=\left(-3\right)^7\)
\(=>n=7\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}=\dfrac{2x-3y+z}{2\cdot9-3\cdot12+20}=\dfrac{6}{2}=3\)
Do đó: x=27; y=36; z=60
\(\dfrac{x}{3}\) = \(\dfrac{y}{4}\) ⇒ \(\dfrac{x}{3.3}\) = \(\dfrac{y}{3.4}\) = \(\dfrac{z}{5.4}\) = \(\dfrac{2x}{2.3.3}\) = \(\dfrac{3y}{3.3.4}\) = \(\dfrac{z}{5.4}\) ⇒ \(\dfrac{2x}{18}\) = \(\dfrac{3y}{36}\) = \(\dfrac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{18}\) = \(\dfrac{3y}{36}\) = \(\dfrac{z}{20}\) = \(\dfrac{2x-3y+z}{18-36+20}\) = \(\dfrac{6}{2}\) = 3
\(x=\) 3 : \(\dfrac{2}{18}\) = 27; y = 3 : \(\dfrac{3}{36}\) = 36; z = 3 x 20 = 60
Vậy ..
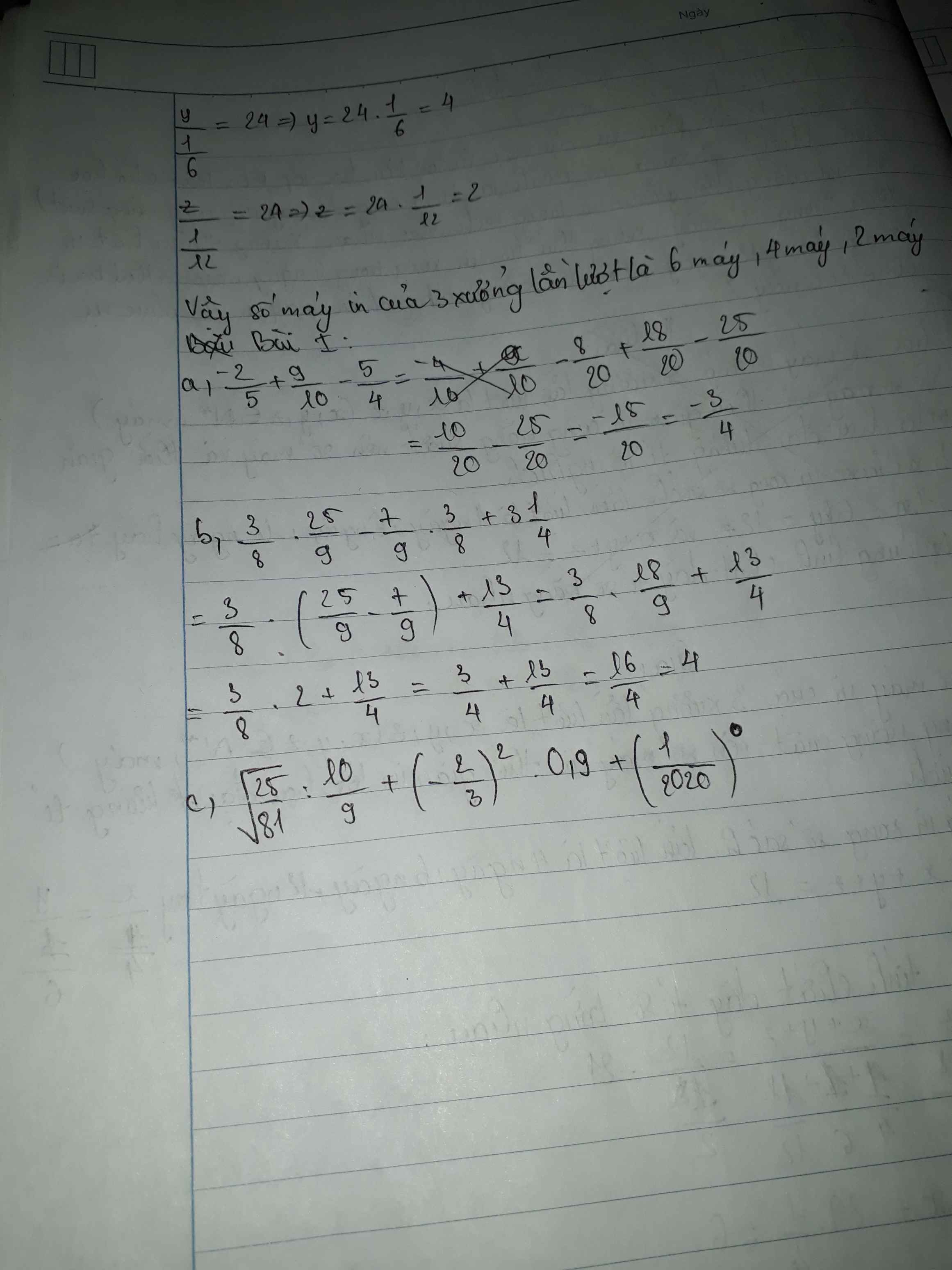
 Giải chi tiết hộ mình nha!!!
Giải chi tiết hộ mình nha!!!
 Giusp mình làm đề này nha!
Giusp mình làm đề này nha!
c: \(=\dfrac{5}{9}\cdot\dfrac{9}{10}+\dfrac{4}{9}\cdot\dfrac{9}{10}+1\)
\(=\dfrac{9}{10}+1=\dfrac{19}{10}\)
Thé 5/9 với 4/9