
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
(x+y+z)^2=9
x+y+z=3 hoặc x+y+z=-3
x(x+y+z)=x.3=-5 =>x=-5/3
Với x+y+z=-3 ta có x=5/3
Tương tự ta cũng có y=3 hoặc y=-3, z=5/3 hoặc z=-5/3

Cộng ba vế trên vế theo vế ta được:
\(x\left(x+y+z\right)+y\left(x+y+z\right)+z\left(x+y+z\right)=-5+9+5\)
\(\Leftrightarrow\left(x+y+z\right)\left(x+y+z\right)=9\)
\(\Leftrightarrow\orbr{\begin{cases}x+y+z=-3\\x+y+z=3\end{cases}}\)
Với \(x+y+z=-3\)
\(\Rightarrow x=\frac{5}{3}\);\(y=-3\);\(z=-\frac{5}{3}\)
Với \(x+y+z=3\)
\(\Rightarrow x=-\frac{5}{3}\);\(y=3\);\(z=\frac{5}{3}\)


x(x+y+z) = -5 (1)
y(x+y+z) = 9 (2)
z(x+y+z) = 5 (3)
Cộng (1) ( 2)và (3) ta có
x(x+y+z) + y(x+y+z) + z(x+y+z) = -5 + 9 +5
=> (x+y+z) (x +y +z) = 9
=> (x+y+z)^2 = 9
=> x+y +z = 3 hoặc x+y +z = - 3
(+) TH1 x + y +z = 3
thay vào (1) ta có : x . 3 = -5 => x = -5/3
thay vào (2) ta có : y . 3 = => y =3
thay vào 3 ta có z . 3 = 5 => z = 5/3
(+) TH2 tương tự
(lik e nha **** hết cho mình đi)

Theo đầu bài ta có:
\(\hept{\begin{cases}x\left(x+y+z\right)=-5\\y\left(x+y+z\right)=9\\z\left(x+y+z\right)=5\end{cases}}\)
\(\Rightarrow x\left(x+y+z\right)+y\left(x+y+z\right)+z\left(x+y+z\right)=-5+9+5\)
\(\Rightarrow\left(x+y+z\right)\left(x+y+z\right)=4+5\)
\(\Rightarrow\left(x+y+z\right)^2=9\)
\(\Rightarrow x+y+z=3\)
\(\Rightarrow\hept{\begin{cases}x=-\frac{5}{x+y+z}=-\frac{5}{3}\\y=\frac{9}{x+y+z}=3\\z=\frac{5}{x+y+z}=\frac{5}{3}\end{cases}}\)

Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
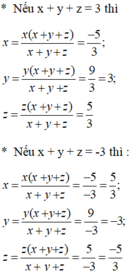

Câu 3:
\(\dfrac{x}{y}=\dfrac{5}{9}\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=5\\ \dfrac{y}{9}=10\Rightarrow y=90\)
Câu b:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\dfrac{x}{2}=7\Rightarrow x=14\\ \dfrac{y}{3}=7\Rightarrow y=21\)
Câu c:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-1}{5+7-10}=\dfrac{20}{2}=10\)
\(\dfrac{x}{5}=10\Rightarrow x=50\\ \dfrac{y}{7}=10\Rightarrow y=70\\ \dfrac{z}{10}=10\Rightarrow z=100\)
Câu d:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\dfrac{x}{3}=11\Rightarrow x=3\\ \dfrac{y}{4}=11\Rightarrow y=44\\ \dfrac{z}{5}=11\Rightarrow z=55\)
Câu e:
\(\dfrac{x}{4}=\dfrac{y}{2}\Rightarrow\dfrac{x}{8}=\dfrac{y}{6}\\\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{y}{6}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10} \)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{8+6-10}=\dfrac{20}{4}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{6}=5\Rightarrow y=30\\ \dfrac{z}{10}=5\Rightarrow z=50\)
3) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.9=90\end{matrix}\right.\)
4) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x}{10}=\dfrac{2y}{6}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)
\(\Rightarrow\left\{{}\begin{matrix}x=7.2=14\\y=7.3=21\end{matrix}\right.\)
5) \(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-z}{5+7-10}=\dfrac{20}{2}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.7=70\\z=10.10=100\end{matrix}\right.\)
6) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x}{9}=\dfrac{2y}{8}=\dfrac{2z}{10}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)
\(\Rightarrow\left\{{}\begin{matrix}x=11.3=33\\y=11.4=44\\z=11.5=55\end{matrix}\right.\)
7) \(\Rightarrow\dfrac{x}{12}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{12+6-10}=\dfrac{20}{8}=\dfrac{5}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}.12=30\\y=\dfrac{5}{2}.6=15\\z=\dfrac{5}{2}.10=25\end{matrix}\right.\)

\(\hept{\begin{cases}x\left(x+y+z\right)=-5\left(1\right)\\y\left(x+y+z\right)=9\left(2\right)\\z\left(x+y+z\right)=5\left(3\right)\end{cases}}\)
Cộng vế của ( 1 ) , ( 2 ) và ( 3 ) ta có
( x+y+z)\(^2\)=9
=>x +y + z = \(\ne\)9
Xét x + y +z = 9
=> \(\hept{\begin{cases}x.9=-5\\y.9=9\\z.9=5\end{cases}}\)
=>\(\hept{\begin{cases}x=\frac{-5}{9}\\y=1\\z=\frac{5}{9}\end{cases}}\)
Xét x + y + z = - 9
=> \(\hept{\begin{cases}x.\left(-9\right)=\left(-5\right)\\y.\left(-9\right)=9\\z.\left(-9\right)=5\end{cases}}\)
=>\(\hept{\begin{cases}x=\frac{5}{9}\\y=-1\\x=\frac{-5}{9}\end{cases}}\)
Tìm x ; y ; z hả !
Ta có: x(x+y+z)= 5; y(x+y+z)= 9; z(x+y+z)= -5
=> x(x + y + z) + y(x + y + z) + z(x + y + z) = 5 + 9 + (-5)
=> (x + y + z)(x + y + z) = 9
=> (x + y + z)2 = 9
=> (x + y + z) = 3 hoặc (x + y + z) = -3
Với (x + y + z) = 3 thì x . 3 = 5 => x = \(\frac{5}{3}\); y . 3 = 9 => y = 3 ; z . 3 = -5 => z = \(\frac{-5}{3}\)
Với (x + y + z) = -3 thì x . (-3) = 5 => x = \(\frac{-5}{3}\); y . 3 = 9 => y = -3 ; z . (-3) = -5 => z = \(\frac{5}{3}\)